If (1+x)(1+x2)(1+x4)(1+x128)=n∑r=0xr then n is equal to 256 b. 255 c. 254 d. none of these
255
127
63
none of these
The correct Answer is:A
We have,
(1+a)(1+a2)(1+a4)....(1+a128)=n∑r=0ar
⇒ n=Exponenet of the highest power of a
⇒ n=1+2+4+....+128
⇒ n=1+2+22+....+27=(28−12−1)=255
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Section II - Assertion Reason Type13videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise129videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test59videos
SEQUENCES AND SERIES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test50videos
QUADRATIC EXPRESSIONS AND EQUATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test30videos
SETS
Similar Questions
If (1+x)(1+x2)(1+x4)….(1+x128)=Σnr=0xr, then n is equal is
View Solutionlimx→1∑nr=1xr−nx−1 is equal to
View SolutionIf (2+x)(2+x2)(2+x3)………..(2+x100)=n∑r=0krxr,then n= (A) 2550 (B) 5050 (C) 28 (D) none of these
View SolutionIf (1+2x+x2)n=2n∑r=0arxr, then ar=
View Solutionlimx→2∑nr=1xr−∑nr=12rx−2 is equal to
View SolutionIf Σ2nr=1sin−1xr=nπ,thenΣ_(r=1)2nxr is equal to
View Solution(1+x)n=n∑r=0Crxr then match the following
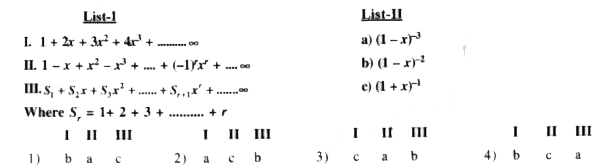 View Solution
View SolutionThe value of n−1∑r=0^nCr/(^nCr+nCr+1) equals a. n+1 b. n/2 c. n+2 d. none of these
View SolutionIf (1+2x+x2)n=2n∑r=0arxr ,then ar is a.(.nC2)2 b. .nCr.nCr+1 c. .2nCr d. .2nCr+1
View SolutionThe coefficient of xn in (1+x)101(1−x+x2)100 is non zero, then n cannot be of the form a. 3r+1 b. 3r c. 3r+2 d. none of these
View Solution

