If $3 sin x + 4 cos x = 5$ , then the value of $90 {tan}^{2} (\frac{x}{2}) - 60 tan (\frac{x}{2}) + 110$ is equal toSolution in Punjabi

Video Solution

Text Solution

Verified by Experts

The correct Answer is:0

Updated on:21/07/2023

Answer

Step by step video & image solution for If 3sinx+4cosx=5, then the value of 90tan^2(x/2)-60tan(x/2)+110 is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC EQUATIONS AND INEQUATIONS

Topper's Solved these Questions

TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Statement I And Ii Type Questions)
6 Videos
TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Matching Type Questions)
2 Videos
TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Trigonometric Equations and Inequations Exercise 3 :Passage Based Questions
1 Videos
THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos

Similar Questions

Evaluate $\int_{0}^{1}$ $\frac{2}{2 x + 12}$ $d x$
View Solution
Evaluate $\int$ $\frac{1}{e^{x}}$ $d x$
View Solution
If an angle and a side of a right angle triangle is known , then rest of the sides and angles can be found as follows
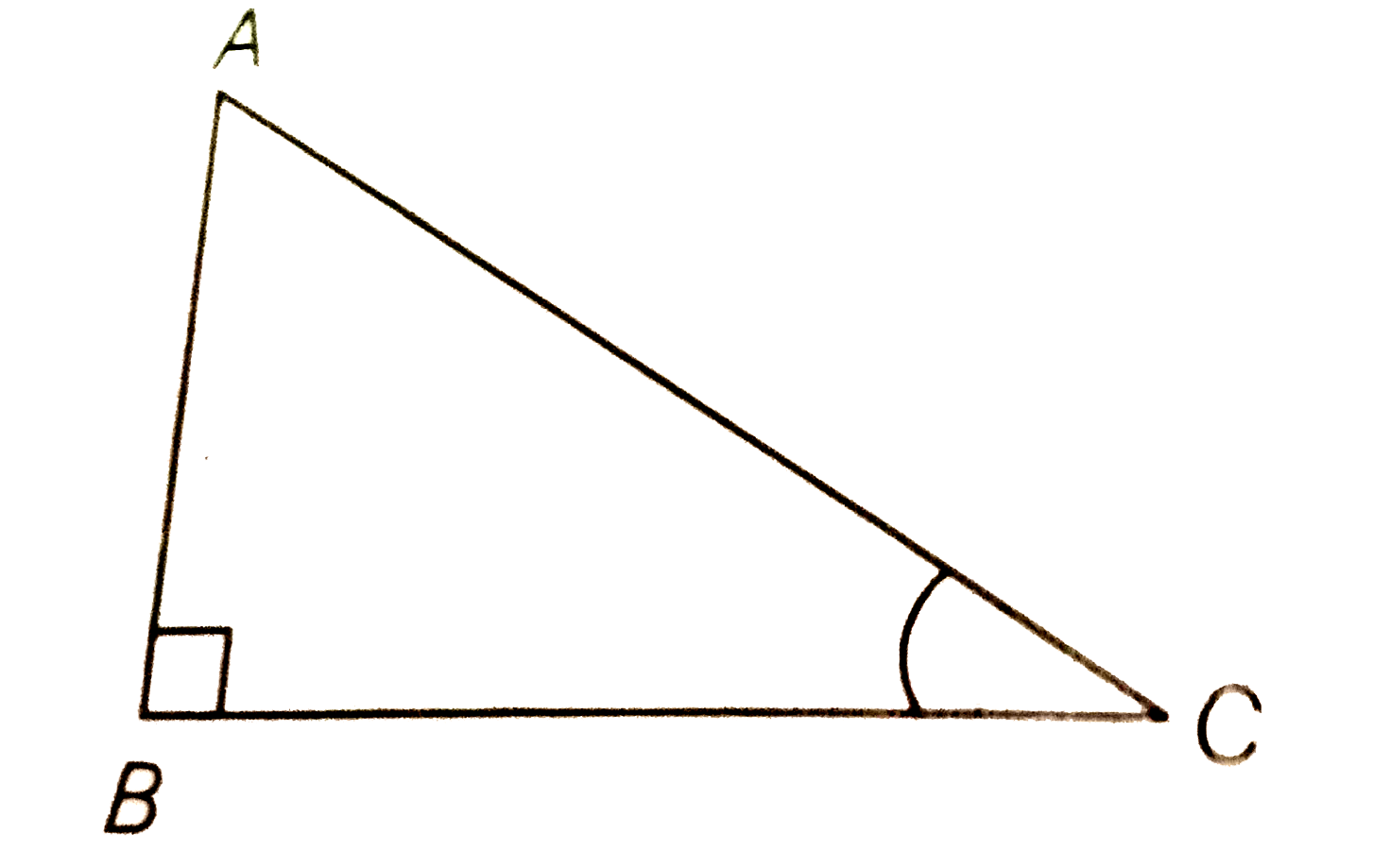
In $Δ A B C$ (figure ), if $∠ B = 90^{\circ}, ∠ C = θ and B C = x$ , then $A B = x tan θ and A C = x sec θ$ .

Now, consider in isosceles triangle PQR (Figure 2),

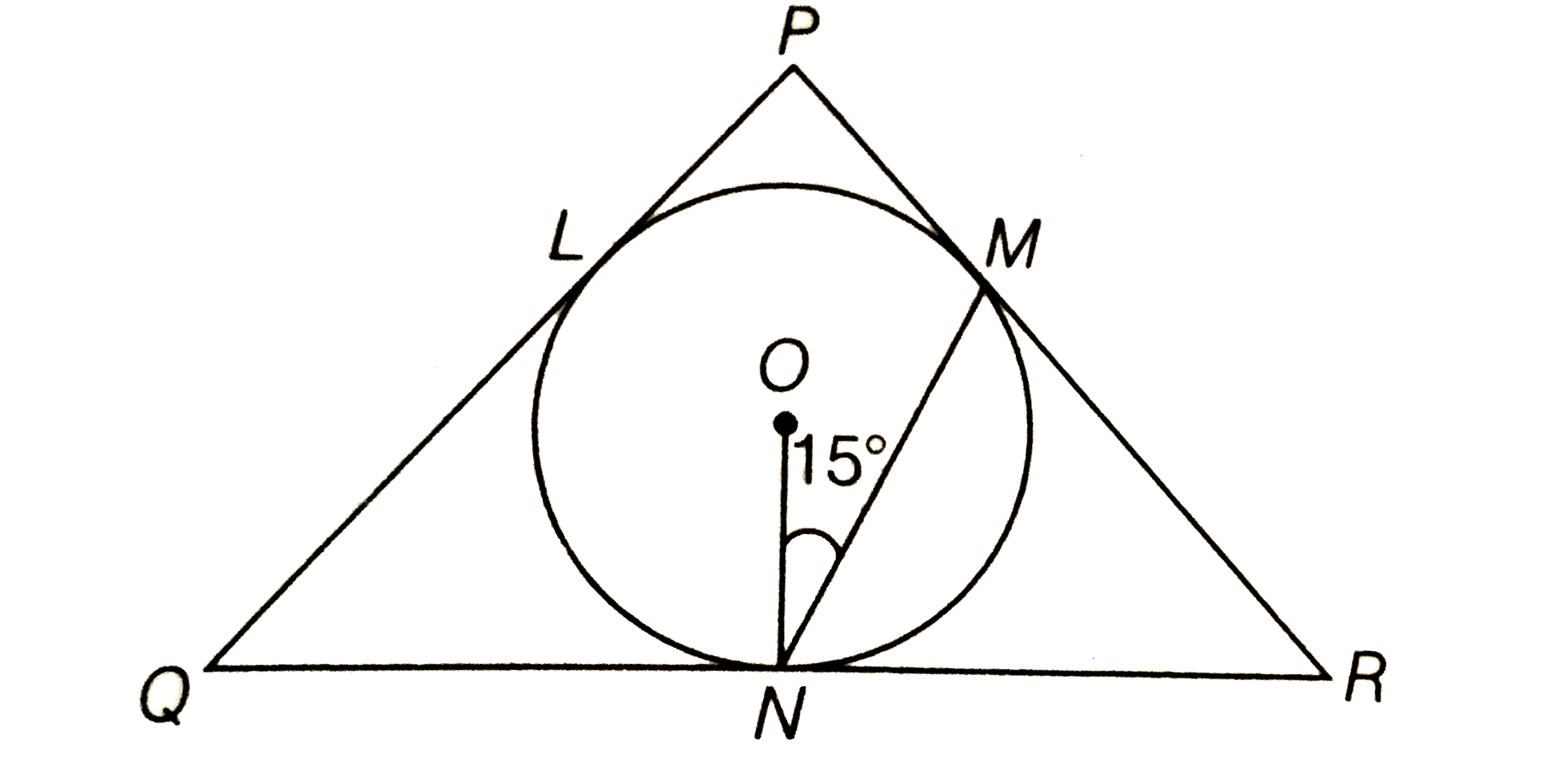
Where PQ=PR and $20 N = \sqrt{3}$
On the basis of the above information answer the question
The angle of triangle PQR are
View Solution
Consider the line $L_{1} : \frac{x - 1}{2} = \frac{y}{- 1} = \frac{z + 3}{1}, L_{2} : \frac{x - 4}{1} = \frac{y + 3}{1} = \frac{z + 3}{2}$ find the angle between them.
View Solution
Let $α and β$ be non-zero real numbers such that $2 (cos β - cos α) + cos α cos β = 1$ . Then which of the following is/are true ?
View Solution
$\int \frac{d x}{3 sin x - 4 cos x + 5}$
View Solution
The maximum value of (3cosx+4sinx) (3sinx-4cosx) for every x $\in$ R is
View Solution
समाकलन कीजिए - $\int (3 sin x - 4 cos x + 5 {sec}^{2} x - 2 cos e c^{2} x) d x$
View Solution
$\int (2^{x} - 4 cos x + 2) d x$ equals
View Solution
সমাকলন করো : $\int \frac{d x}{{(3 sin x + 4 cos x)}^{2}}$
View Solution
The minimum value of $\sqrt{(3 sin x - 4 cos x - 10) (3 sin x + 4 cos x - 10)}$ is ________
View Solution
The minimum value of $\sqrt{(3 s \in x - 4 cos x - 10 (3 sin x + 4 cos x - 1))}$ is ________
View Solution
$3 sin x + 4 cos x - 6 = 0$ then the general solution of x =
View Solution
If $3 sin x + 4 cos x = 5$ then the value of $tan (x / 2)$ is
View Solution
$\frac{x + 1}{{(x - 1)}^{2} (x - 2)} =$
View Solution
Find the maximum value of the $2 + 3 sin x + 4 cos x$
View Solution

ARIHANT MATHS-TRIGONOMETRIC EQUATIONS AND INEQUATIONS-Exercise (Single Integer Answer Type Questions)

Evaluate int(0)^(1)1/(x+1)dx
01:26
If the sum of the root of the equation cos 4x + 6+7 cos 2x in the in...
04:30
Find dy/dx if ax+by^2=cosy
02:58
Number of ordered pair (x,y) which satisfies the relation (x^(4)+1)/(...
09:21
Find dy/dx if sin(x-y)=3x
02:20
The value of sin(cot^-1x) is equal to
02:06
Let p,qin N and q gt p, the number of solutions of the equation q|sin...
03:12
If theta(1),theta(2),theta(3) are three values lying in [0,3pi) for wh...
05:17
If alpha be the smallest positive root of the equation sqrt(sin(1-x...
04:56
Find the sum of all real values of X satisfying the equation (x^2-5x+5...
07:17
If tan(pi cos theta )= cot (pi sin theta ) ,then cos^(2)(theta -pi/...
02:57
If 3sinx+4cosx=5, then the value of 90tan^2(x/2)-60tan(x/2)+110 is equ...
03:17

Home
Ask Doubt
Profile

If 3sinx+4cosx=5, then the value of 90tan2(x2)−60tan(x2)+110 is equal toSolution in Punjabi

The correct Answer is:0

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS-TRIGONOMETRIC EQUATIONS AND INEQUATIONS-Exercise (Single Integer Answer Type Questions)

If $3 sin x + 4 cos x = 5$ , then the value of $90 {tan}^{2} (\frac{x}{2}) - 60 tan (\frac{x}{2}) + 110$ is equal toSolution in Punjabi