If (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then (a)e=√38612 (b) e=√38613 (c)LR=1216 (d) LR=1213Solution in Bengali
e=√38612
e=√38613
LR=121/6
LR=121/3
The correct Answer is:A, C
We have foci S1(5,12)andS2(24,7).
Hyperbola passes through P(0, 0).
∴ |PS1−PS2|=2a
2a=K
or 2a=∣∣∣√(24−0)2+(7−0)2−√122+52∣∣∣=12
∴ a=6
S1S2=2ae=√(24−5)2+(12−7)2=√386
∴ e=√38612
LR=2b2a=2a2(e2−1)a
=2×6(386144−1)=1216
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMOREHENSION TYPE21videos
HYPERBOLA
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - MATRIX MATHC TYPE10videos
HYPERBOLA
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - EXERCISES68videos
HYPERBOLA
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Multiple Correct Answer Type2videos
INDEFINITE INTEGRATION
Similar Questions
Consider an ellipse x2a2+y2b2=1 Let a hyperbola is having its vertices at the extremities of minor axis of an ellipse and length of major axis of an ellipse is equal to the distance between the foci of hyperbola. Let e1 and e2 be the eccentricities of an ellipse and hyperbola respectively. Again let A be the area of the quadrilateral formed by joining all the foci and A, be the area of the quadrilateral formed by all the directrices. The relation between e1ande2 is given by
05:26View SolutionLet the foci of the hyperbola X2A2−y2B2=1 be the vertices of the ellipse x2a2+y2b2=1 and the foci of the ellipse be the vertices of the hyperbola. Let the eccentricities of the ellipse and hyperbola be eE and eH, respectively. Then match the following lists.
 02:13View Solution
02:13View SolutionIf the distance between the foci and the distance between the two directricies of the hyperbola x2a2−y2b2=1 are in the ratio 3:2, then b:a is (a)1:√2 (b) √3:√2 (c)1:2 (d) 2:1
04:05View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
02:10View SolutionIf ∫e4x−1e2xlog(e2x+1e2x−1)dx=t22logt−t24−u22logu+u24+C, then
05:48View SolutionIf (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then e=√38612 (b) e=√38613 LR=1216 (d) LR=1213
01:42View SolutionThe foci of the hyperbola 3(y−1)2−4(x−2)2=12 are (0,√7) b. (−2,1−√7) c. 2,1−√7 d. (0)−√7
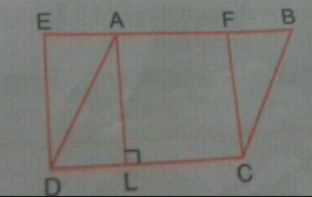
02:29View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
 01:19View Solution
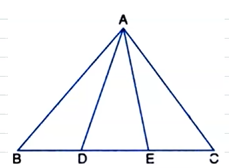
01:19View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
 06:20View Solution
06:20View SolutionLet R be a relation on N×N defined by (a,b) R(c,d)⇔a+d=b+c for all (a,b),(c,d)∈N×N show that: (i) (a,b)R (a,b) for all (a,b)∈N×N (ii) (a,b)R(c,d)⇒(c,d)R(a,b)for all (a,b), (c,d)∈N×N (iii) (a,b)R (c,d)and (c,d)R(e,f)⇒(a,b)R(e,f) for all (a,b), (c,d), (e,f)∈N×N
05:20View Solution√24÷0.5+1+√18÷0.6+6=? (a) 19 (b) 13 (c) 12 (d) 15
03:41View Solutionb 3 P, c 6 R, d 12 T, e 24 V, ?
03:17View SolutionIf (5,12) and (24,7) are the foci of a hyperbola passing through the origin , then the eccentricity of the hyperbola is :
04:01View SolutionIf (5,12), (24,7) are the foci of the hyperbola passing through origin, then its eccentricity is
03:31View SolutionIf (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then e=√38612 (b) e=√38613 LR=1216 (d) LR=1213
03:24View SolutionIf (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then e=√38612 (b) e=√38613 LR=1216 (d) LR=1213
04:16View Solution

