If A = {1, 2, 3} and B = {3, 8}, then (A∪B)×(A∩B)is
{(3, 1), (3, 2), (3, 3), (3, 8)}
{(1, 3), (2, 3), (3, 3), (8, 3)}
{(1, 2), (2, 2), (3, 3), (8, 8)}
{(8, 3), (8, 2), (8, 1), (8, 8)}
The correct Answer is:B
To solve the problem, we need to find the Cartesian product of the union and intersection of two sets A and B. Let's break it down step by step.
Step 1: Define the Sets
Given:
- A={1,2,3}
- B={3,8}
Step 2: Find the Union of Sets A and B
The union of two sets combines all unique elements from both sets.
A∪B={1,2,3}∪{3,8}
Here, we take all elements from both sets without repetition:
A∪B={1,2,3,8}
Step 3: Find the Intersection of Sets A and B
The intersection of two sets includes only the elements that are present in both sets.
A∩B={1,2,3}∩{3,8}
The common element is:
A∩B={3}
Step 4: Find the Cartesian Product of A∪B and A∩B
The Cartesian product of two sets X and Y is the set of all ordered pairs (x,y) where x is from set X and y is from set Y.
(A∪B)×(A∩B)={1,2,3,8}×{3}
We will create pairs by taking each element from A∪B and pairing it with the element from A∩B:
- Pairing 1 with 3: (1,3)
- Pairing 2 with 3: (2,3)
- Pairing 3 with 3: (3,3)
- Pairing 8 with 3: (8,3)
Thus, the Cartesian product is:
(A∪B)×(A∩B)={(1,3),(2,3),(3,3),(8,3)}
Final Answer
The result of (A∪B)×(A∩B) is:
{(1,3),(2,3),(3,3),(8,3)}
Given:
- A={1,2,3}
- B={3,8}
The union of two sets combines all unique elements from both sets.
A∪B={1,2,3}∪{3,8}
Here, we take all elements from both sets without repetition:
A∪B={1,2,3,8}
The intersection of two sets includes only the elements that are present in both sets.
A∩B={1,2,3}∩{3,8}
The common element is:
A∩B={3}
The Cartesian product of two sets X and Y is the set of all ordered pairs (x,y) where x is from set X and y is from set Y.
(A∪B)×(A∩B)={1,2,3,8}×{3}
We will create pairs by taking each element from A∪B and pairing it with the element from A∩B:
- Pairing 1 with 3: (1,3)
- Pairing 2 with 3: (2,3)
- Pairing 3 with 3: (3,3)
- Pairing 8 with 3: (8,3)
(A∪B)×(A∩B)={(1,3),(2,3),(3,3),(8,3)}
The result of (A∪B)×(A∩B) is:
{(1,3),(2,3),(3,3),(8,3)}
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (More Than One Correct Option Type Questions)
3 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Passage Based Questions)
6 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 3
10 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
17 Videos
Similar Questions
If A = {1, 2, 3}, B = {3, 4, 5}, then (A∩B)×A is
View SolutionIf A = {2, 4) and B = {3, 4, 5), then (A∩B)×(A∪B) is
View SolutionIf A = {1, 2, 3) and B = {m, n}, find A×B and B×A. Are these two products equal ?
View SolutionLet A ={2,4,6,8,10}andB={3,6,9}F∈dA uu B .
View SolutionIf A={a,b},B={2,3}andC={3,4}, then evaluate:
(i) A×(B∩C) (ii)A×(B∪C)
View SolutionThe probabilities of outcomes of a random experiment are given below :
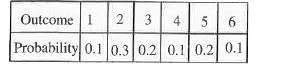
Let A = {2, 4, 6}, B = {1, 2, 3, 4} and C = {1, 2}. Then find P(A), P(B), P( C ), P(A∩B),P(B∩C) and P(C∩A).
View SolutionLet A = { 2,3,4,5,6 } and B = { 4,6,8,10 } Find A∪B
View SolutionIf A={1,2,3,4,5}, B={1,2,3,6,7} and C{8}, then find (A-B)×C.
View SolutionIf A and B are two sets, then A∩(A∪B) equals
View SolutionIf A and B are two sets, then A∩(A∪B) equals
View Solution
