Question

If A, B are two sets, prove that $A\cup B=(A-B)\cup (B-A)\cup (A\cap B)$.
Hence or otherwise prove that
$n(A\cup B)=n\left(A\right)+n\left(B\right)-n(A\cap B)$
where, n(A) denotes the number of elements in A.

Explanation

Let `x inAuuBimpliesx inAorx inB`
`iff(x inAandxcancelinB)or(x inBandxcancelinA)`
or `(x inAandx inB)` [from definition of union]
`iff x in(A-B)orx in(B-A)orx inAnnB`
`iff x in(A-B)uu(B-A)uu(AnnB)`
`therefore AuuBsube(A-B)uu(B-A)uu(AnnB)`
and `(A-B)uu(B-A)uu(AnnB)subeAuuB`
Hence, `AuuB=(A-B)uu(B-A)uu(AnnB)`
Let the common elements in A and B are z and only element of A are x (represented by vertical lines in the Venn diagram) and only element of B are y (represented by horizontal lines in the Venn diagram)

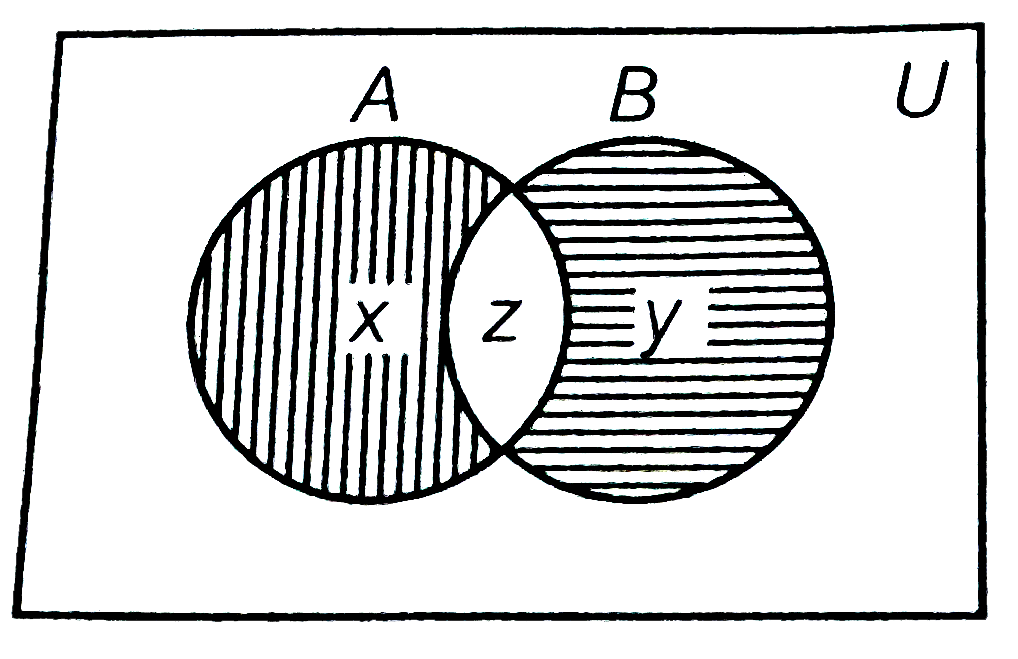
`therefore n(A)` = Total elements of A = x + z
n(B) = Total elements of B = y + z
`n(AnnB)` = Common elements in A and B = z
Now, `n(AuuB)` = Total elements in complete region of A and B
x + y + z
`=(x+z)+(y+z)-z`
`=n(A)+n(B)-n(AnnB)`
Hence, `n(AuuB)=n(A)+n(B)-n(AnnB)`