If a+bxa−bx=b+cxb−cx=c+dxc−dx(x≠0),then show that a, b, c and d are in G.P.
Step by step video & image solution for If (a+b x)/(a-b x)=(b+c x)/(b-c x)=(c+dx)/(c-dx)(x!=0),then show that a, b, c and d are in G.P. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If a+bxa−bx=b+cxb−cx=c+dxc−dx(x≠0) , then show that a, b, c and d are in G.P.
View SolutionIf a+bxa−bx=b+cxb−cx=c+dxc−dx(x≠0) , then show that a, b, c and d are in G.P.
View Solution(xaxb)a+b.(xbxc)b+c.(xcxa)c+a
View SolutionIf x4(x−a)(x−b)(x−c)=P(x)+Ax−a+Bx−b+Cx−c then P(x)=
View SolutionIf a, b are the roots of equation x2−3x+p=0 and c, d are the roots of x2−12x+q=0 and a, b, c, d are in G.P., then prove that :
p : q =1 : 16
View SolutionIf x, a, b, c are real and (x−a+b)2+(x−b+c)2=0, then a, b, c are in
View SolutionIf ax=by=cz and a,b,c are in G.P. show that 1x,1y,1z are in A.P.
View SolutionIf the determinant ∣∣ ∣∣ab2aα+3bbc2bα+3c2aα+3b2bα+3c0∣∣ ∣∣=0 then (a)a,b,c are in H.P. (b)α is root of 4ax2+12bx+9c=0 or(c) a,b,c are in G.P. (d)a,b,c, are in G.P. only a,b,c are in A.P.
View SolutionIf the roots of equation a(b−c)x2+b(c−a)x+c(a−b)=0 be equal prove that a,b,c are in H.P.
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
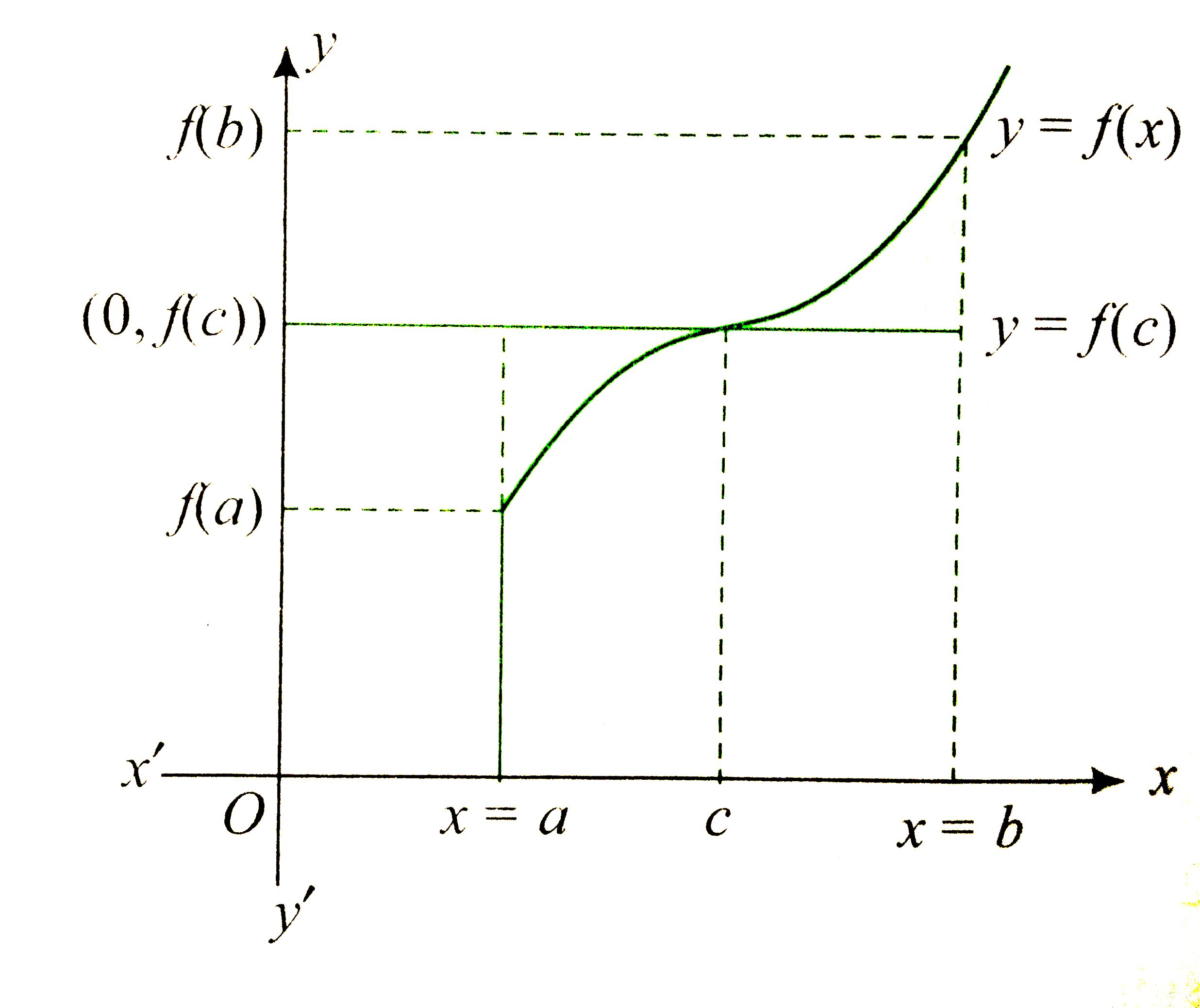
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
View Solution
