If a fair coin is tossed thrice find the probability that there are
at most one tailSolution in Bengali
Let an be the number of strings of H and T of length n with no two adjacent H's.
Then a1=2 (H or T) and a2=3 (HT, TH, T T)
Now consider an+2.
Also, an+2=an+1+an (∵ The string must begin with T or HT)
So, a3=5,a4=8,a5=8+5=13.
Hence, the required probability = 1325=1332
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.2
19 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
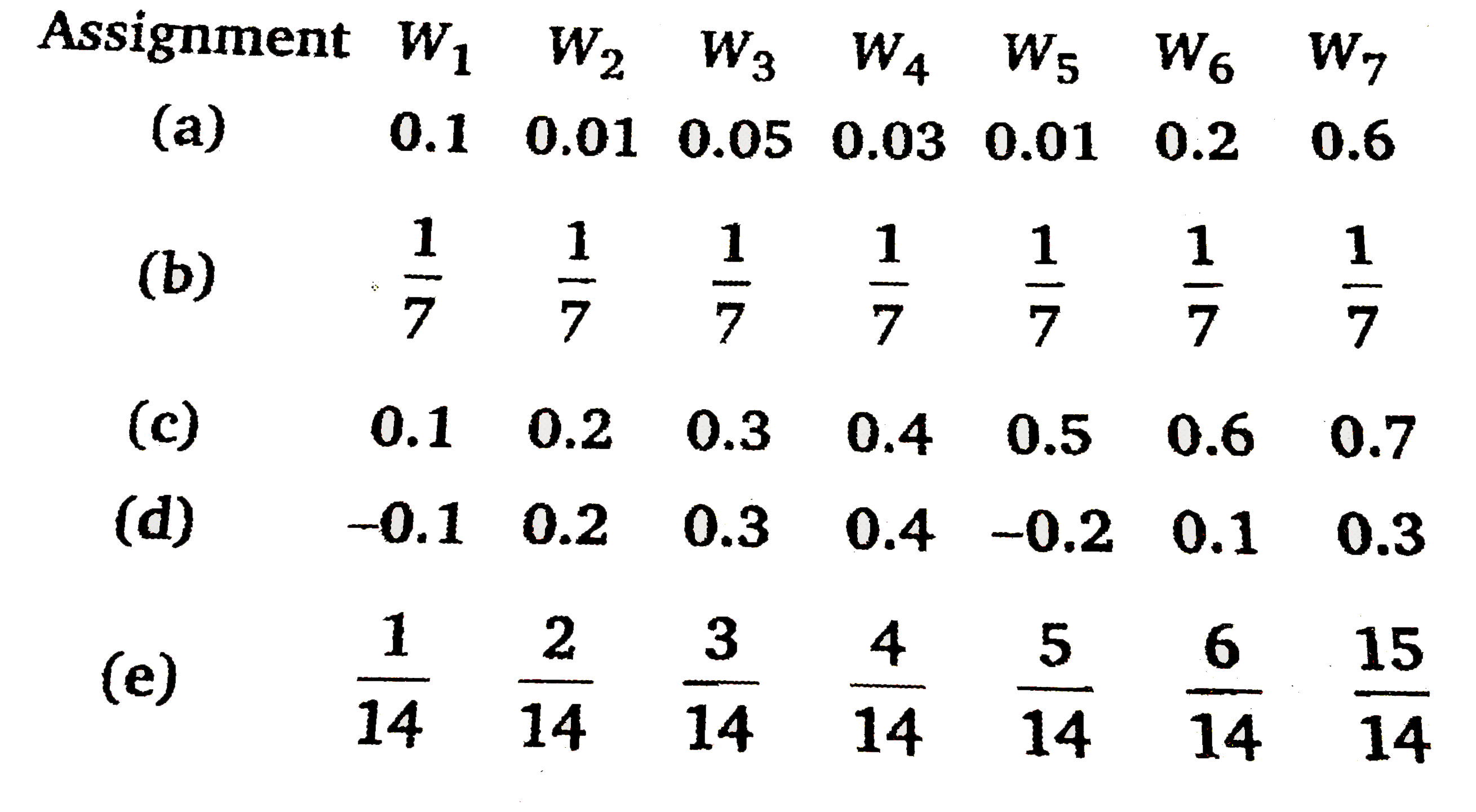
View SolutionIf two fair dices are thrown and digits on dices are a and b, then find the probability for which ωab=1, (where ω is a cube root of unity).
View SolutionLet ω be a complex cube root unity with ω≠1. A fair die is thrown three times. If r1,r2andr3 are the numbers obtained on the die, then the probability that ωr1+ωr2+ωr3=0 is 1/18 b. 1/9 c. 2/9 d. 1/36
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionA fair coin is tossed repeatedly. If tail appears on first four tosses, then find the probability of head appearing on fifth toss.
View SolutionWhen a fair coin is tossed thrice, the probability of obtaining head at most twice is
View SolutionA fair coin is tossed three times . The probability that there is atleast one tail is
View SolutionThree fair coins are tossed. Find the probability that the outcomes are all tails, if atleast one of the coins shows a tail.
View SolutionIf two coins are tossed simultaneously, then find the probability of getting
(i) one had and one tail
(ii) at most two tails
View SolutionThree fair coins are tossed together. Find the probability of getting ' all tails'.
View Solutionthree fair coins are tossed simultaneously . Find the propability of
getting one tail .
View SolutionThree fair coins are tossed. Find the probability that they are all tails, if one of the coins shows a tail.
View SolutionA fair coin is tossed repeatedly. If tail appears on first four tosses, then find the probability of head appearing on fifth toss.
View SolutionA fair coin is tossed repeatedly. If tail appears on first four tosses, then find the probability of head appearing on fifth toss.
View SolutionA fair coin is tossed repeatedly. If tail appears on first four tosses, then find the probability of head appearing on fifth toss.
View Solution
