If a∈R and the equation −3(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer ≤x) has no integral solution, then all possible values of a lie in the interval: (1) (-2,-1) (2) (∞,−2)∪(2,∞) (3) (−1,0)∪(0,1) (4) (1,2)
(−1,0)∪(0,1)
(1,2)
(−2,−1)
(−∞,−2)∪(2,∞)
The correct Answer is:A
a2=3t2−2t, where t={x}∈[0,1)
∴a2=3t(t−2/3)
Graph of f(t)=3t(t−2/3) is as shown in the following figure.
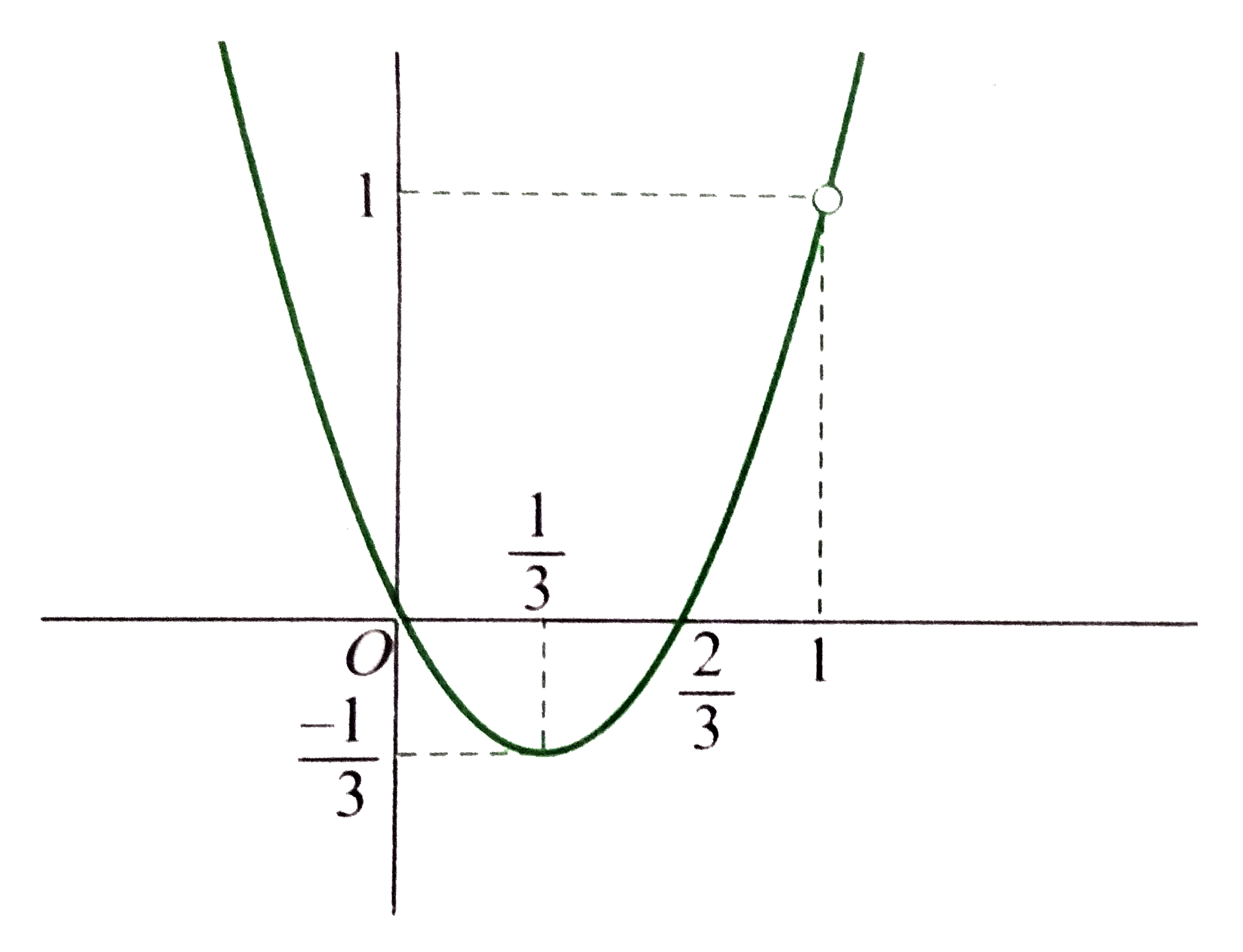
Clearly, from graph
0<a2<1
ora∈(−1,0)∪(0,1)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Solved Examples And Exercises498videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Numerical)31videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank31videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
If a∈R and the equation −3(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer x) has no integral solution, then all possible values of a lie in the interval (1) (−1,0)∪(0,1) (2) (1, 2) (3) (−2,−1) (4) (−∞,−2)∪(2,∞)
View SolutionIf a∈R and the equation −3(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer x) has no integral solution, then all possible values of a lie in the interval (1) (−1,0)∪(0,1) (2) (1, 2) (3) (−2,−1) (4) (−∞,−2)∪(2,∞)
View Solution
Knowledge Check
- Question 1 - Select One
If a ∈ R and the equation (a−2)(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer function) has no integral solution and has exactly one solution in (2, 3), then a lies in the interval
A(−1,2)B(0, 1)C(−1,0)D(2, 3) - Question 2 - Select One
If [x] denotes the greatest integer ≤x , then number of solutions of the equation x2−2−2[x]=0 is
A4B2C3Dnone of these - Question 3 - Select One
The value of the integral, ∫31[x2−2x–2]dx , where [x] denotes the greatest integer less than or equal to x, is :
A−√2−√3+1B−√2−√3−1C-5D−4
If f(x)={x[x],0≤x≤2and(x−1)[x],2≤x≤3 , where [x] denotes the greatest integer function, then
View SolutionEvaluate
∫∞0[3x2+1]dx
where [.] denotes the greatest integer function.View SolutionFind the values of x graphically satisfying [x]−1+x2≤0 where [.] denotes the greatest integer function.
View SolutionIf [x] denotes the greatest integer less than or equal to x, then evaluate (lim)n→∞1n3{[12x]+[22x]+[32x]+}[n2x]}
View SolutionThe domain of f(x)=log12log4log3[x−λ]2 (where [ ] denotes the greatest integer function) is (−∞,2]∪[6,∞) then the value of λ is
View Solution

