If a ≠b≠0, prove that points (a,a2),(b,b2), and (0, 0) can never be collinear. Solution in Kannada
Step by step video & image solution for If a ne b ne0, prove that points (a, a^(2)), (b, b^(2)), and (0, 0) can never be collinear. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - LONG ANSWER [LA] TYPE QUESTIONS
6 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - HIGHER ORDER THINKING SKILLS [HOTS] QUESTIONS
14 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - VERY SHORT ANSWER [VSA] TYPE QUESTIONS
14 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
9 Videos
- CONSTRUCTIONSBOOK - ZEN PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS) IIT /OLYMPIAD/ IMO
5 Videos
Similar Questions
The vertices of AABC are A(4, 6), B(1, 5), and C7, 2). A line is drawn to intersect sides AB and AC at D and E respectively. Show that ADAB=AEAC=14. Find the area of Δ ADE and compare it with Δ ABC.
View SolutionIn what ratio does 4x +3y-13 0 divide the line segment joining (2, 1) and (1, 4)?
View SolutionFind the area of the triangle Δ ABC with A(a,b+c), B(b,c+a), and C(c, a+ b).
View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
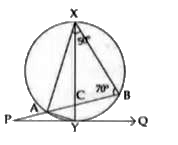
View SolutionGiven below are the steps of construction of a pair of tangents to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm. Find which of the following steps is wrong.
(P) Step 1: Take a point O on the plane paper and draw a circle of radius OA = 4 cm. Also draw a concentric circle of radius OB = 6 cm.
(Q) Step 2: Find the midpoint C of OB and draw a circle of radius BA= AO. Suppose this circle intersects the circle of radius 4 cm at P and Q.
(R) Step 3: Join BP and BQ to get the desired tangents.
View SolutionIf the points (a,0),(0,b) and (3,2) are collinear,prove that (2)/(b)+(3)/(a)=
View Solution[(a0+b0)(a0−b0)a2−b2]0+5 (where a≠0andb≠0) is
View SolutionIf a≠b≠c,prove that(a,a2),(b,b2),(0,0) will not be collinear.
View Solutionयदि a≠b≠0, तो सिध्द कीजिए कि बिंदु (a,a2),(b,b2),(0,0) संरेख नहीं होंगे ।
View SolutionThe points (−a,−b),(a2,ab),(a,b),(0,0),a≠0,b≠0 are always
View SolutionIf a=b2c, where a≠0 and b≠0 , then bc=
View SolutionFind the condition for the points (a,0),(h,k) and (0,b) when ≠0 to be collinear.
View SolutionIf a and b are the roots of the equation x2+ax+b=0,a≠0,b≠0, then the values of a and b are respectively
View SolutionIf ∣∣ ∣∣ab00abb0a∣∣ ∣∣ = 0, (a≠0) then
View Solutionयदि a≠0,b≠0 और |a+b|=|a−b|, तो सदिश a और b हैं
View Solution
