If a parallelogram ABCD, |AB|=a,|AD|=band|AC|=C, then DA. AB is equal to
12(a2+b2+c2)
12(a2−b2+c2)
14(a2+b2−c2)
13(b2+c2−a2)
The correct Answer is:A
We have, |AB|=a,|AD|=b,|AC|=c

In ΔABC, AB+BC=AC
⇒AB+AD=AC [∵BC=AD]
⇒AB−DA=AC [∵AD=−DA]
⇒|AB−DA|=|AC|
⇒|AB−DA|2=|AC|2
⇒|AB|2+|DA|2−2AB⋅DA=(AC)2
⇒a2+b2−2AB⋅DA=c2 [∵|AD|=|DA|=b]
⇒2DA⋅AB=a2+b2−c2
⇒DA⋅AB=12[a2+b2−c2]
Topper's Solved these Questions
- VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - VECTORS EXERCISE - ( MHT CET Corner)
66 Videos
- VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - VECTORS EXERCISE - ( MHT CET Corner)
66 Videos
- TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLESEXERCISE - Exercise 2 (MISCELLANEOUS PROBLEMS)
20 Videos
Similar Questions
Knowledge Check
In a parallelogram ABCD, AB = 12 cm and the altitude corresponding to AB is 8 cm. If AD= 10 cm, then the altitude corresponding to AD is equal to
A8.5 cmB9 cmC9.6 cmD10.8 cmIn △ABC,AB=AC and∠B=65∘ then ∠C is equal to
A130∘B32∘C70∘D65∘
ABCD is a quadrilateral with ¯¯¯¯¯¯AB=¯a,¯¯¯¯¯¯AD=¯b,¯¯¯¯¯¯AC=2¯a+3¯b . If the area of parallelogram ABCD is p times the area of the parallelogram with AB,AD as adjacent sides, then p is equal to
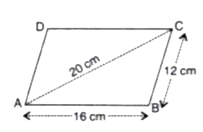
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionConstructed a parallelogram ABCD, when :
AB=4.4cm,AD=6.2cmandAC=4.8cm.
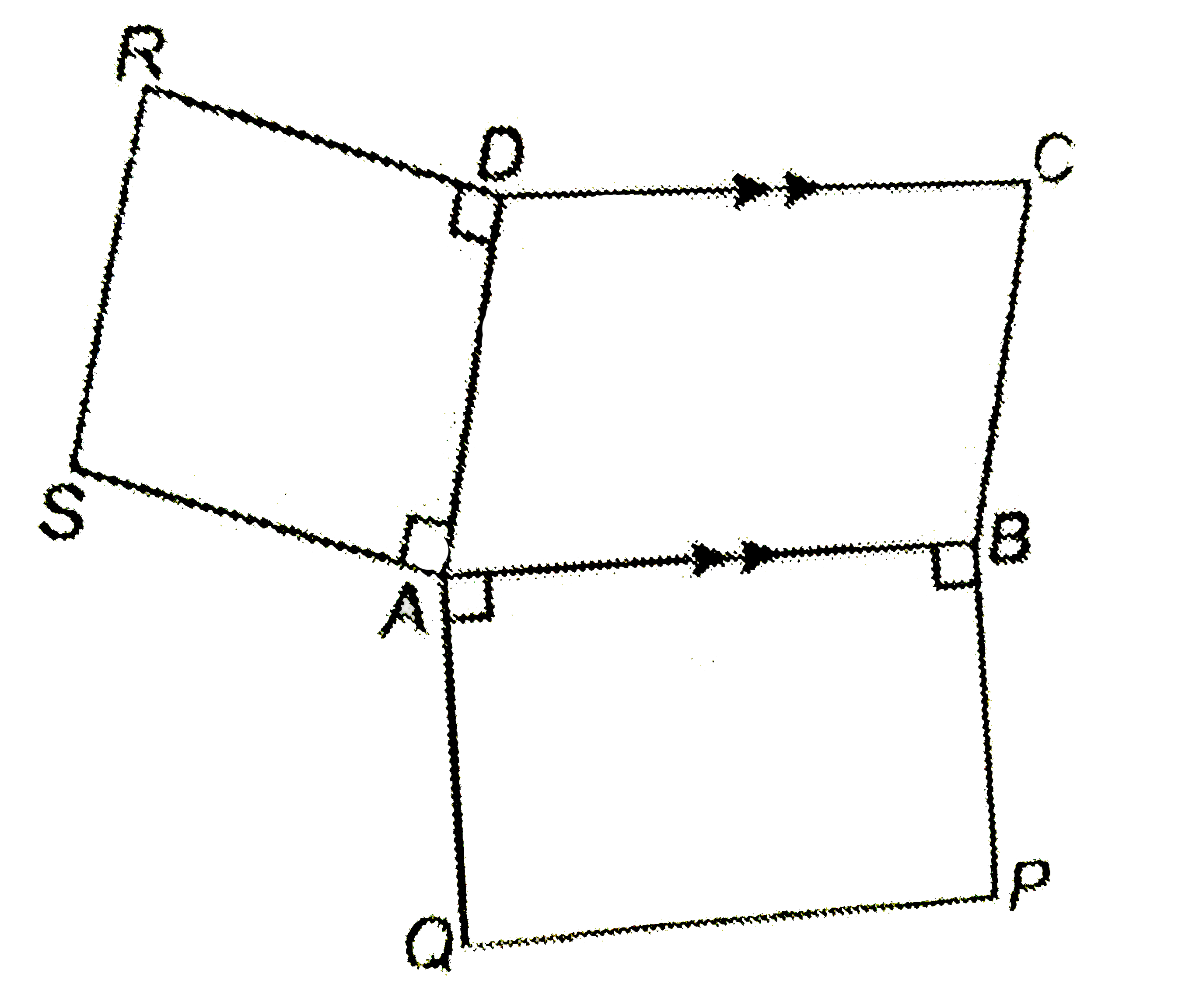
View SolutionThe given figure showns a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD respectively of the parallelogram ABCD. Prove that :
(i) ∠SAQ=∠ABC
(ii) SQ=AC
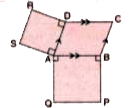
View SolutionThe given figure shows a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD of the parallelogram ABCD. Prove that :
(i) ∠SAQ=∠ABC
(ii) SQ = AC
View SolutionIn a parallelogram ABCD, the bisector of ∠A bisects the line B at point X. Prove that AD = 2AB.
View Solution
