If a point C lies between two points A and B such that AC = BC, then prove that AC=12AB. Explain by drawing the figure.

We have, AC = BC,
Adding AC on both sides, we get
AC+AC=BC+AC (if equals added to equals then wholes are equal)
⇒ 2AC=AB (∵AC+CB=AB)
⇒ AC=12AB Hence Proved.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise3videos
INTRODUCTION TO EUCLID'S GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise3videos
INTRODUCTION TO EUCLID'S GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise11videos
HERONS'S FORMULA
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise12videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
If a point C lies between two points A and B such that AC = BC, then prove that AC=12AB. Explain by drawing the figure.
 View Solution
View SolutionIf A. B and C are three points on a line, and B lies between A and C then prove that AB−BC=AC.
View SolutionIf A, B and C are three points on a line and B is between A and C then prove that AC - BC = AB.
 View Solution
View SolutionIf A, B and C are three poins on a line and B lies between A and C, then prove that AB + BC = AC.
 View Solution
View SolutionIf A, B and C are three poins on a line and B lies between A and C, then prove that AB + BC = AC.
 View Solution
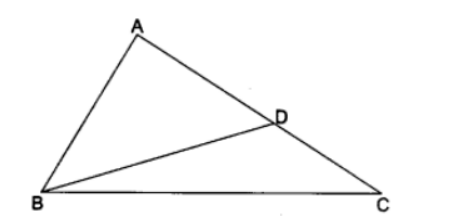
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
 View Solution
View SolutionIf A, B and C are three points on a line, and B lies between A and C (see figure), then prove that AB + BC = AC.
 View Solution
View SolutionPoint C lies on a segment joining the points A(1,1) and B(2,-3)
and 3AC = BC . Find the coordinates of point C ,View SolutionDraw any line segment, say AB. Take any point C lying in between AandB. Measure the lengths of AB,BCandAC.IsAB=AC+CB [Note : If A,B,C are any three points on a line such that AC+CB=AB , then we can be sure that C lies between AandB.
View SolutionB is a point on line segment AC such that AB: BC is 3 : 2. If AC = 40 cm, then length of BC is
View Solution

