If a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid and the incenter of the triangle.
Let E and F be the midpoints of AB and AC. Let the coordinates of B and C be (α,β) and (γ,δ) respectively. Then −2=1+α2,3=1+β2,
5=1+γ2,2=1+δ2
∴α=−5,β=5,γ=9,δ=3
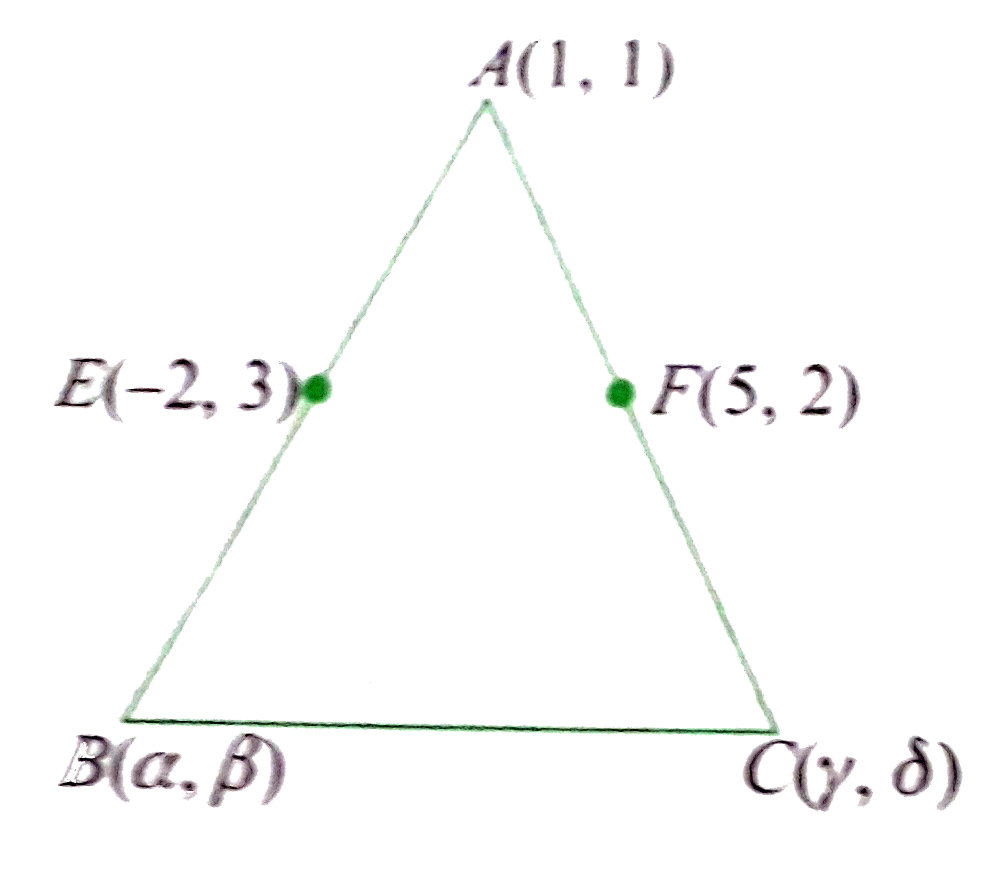
Therefore, the coordinates of B and C are (−5,5) and (9,3), respectively.
Then the centroid is
(1−5+93,1+5+93)≡(53,3)
and a=BC=√(−5−9)2+(5−3)2=10√2
b=CA=√(9−1)2+(3−1)2=2√17
c=AB=√(1+5)2+(1−5)2=2√13
Then, the incenter is
(10√2(1)+2√17(−5)+2√13(9)10√2+2√17+2√13,10√2(1)+2√17(5)+2√13(3)10√2+2√17+2√13)
i.e., (5√2−5√17+9√135√2+√17+√13,5√2+5√17+3√135√2+√17+√13)
Similar Questions
If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (−2, 3) and (5, 2) , find the other vertices.
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View Solution
Knowledge Check
If a vertex of a triangle be (1,1) and the middle points of the two sides through it be (-2,3) and (5,2) then the centroid of the triangle is
A(53,3)B(53,−3)C(−53,3)D(−53,−3)If a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
A(1,73)B(13,73)C(−13,73)D(−1,73)If the middle points of the sides of a triangle be (- 2, 3), (4, - 3) and (4, 5), then the centroid of the triangle is:
A(5/3, 2)B(5/6, 1)C(2, 5/3)D(1, 5/6)
21. If a vertex of a triangle is (1, 1) and the midpoints of two sides of the triangle through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle is
View SolutionIf a vertex of a triangle is (1,1) and the mid-points of two sides through the vertex are (-1,2) and (3,2), then the centroid of the triangle is
View SolutionIf the vertex of a triangle is (1 , 1) and the midpoints of two sides of the triangle through this vertex are (-1 , 2 ) and (3 , 2) , then the centroid of the triangle is :
View SolutionIf the vertex of a triangle is (1 , 1) and the midpoints of two sides of the triangle through this vertex are (-1 , 2 ) and (3 , 2) , then the centroid of the triangle is :
View SolutionIf the middle points of the sides of a triangle are (−2,3),(4,−3),and(4,5) , then find the centroid of the triangle.
View Solution
