If a wire in the shape of a square is rebent into a rectangle, then the _____ of both shapes remain same, but ______ may vary.
To solve the question, we need to understand the relationship between the perimeter and area of a square and a rectangle formed from the same wire.
1. Understanding the Shapes:
- We start with a wire shaped like a square. Let's denote the length of one side of the square as s.
- The perimeter of a square is given by the formula:
Perimeter of Square=4s
2. Re-bending the Wire:
- When the wire is re-bent into a rectangle, it will still have the same length as the perimeter of the square.
- Therefore, the perimeter of the rectangle will also be:
Perimeter of Rectangle=4s
3. Area Calculation:
- The area of the square can be calculated using the formula:
Area of Square=s2
- For the rectangle, let’s denote the length as l and the breadth as b. The perimeter of the rectangle can be expressed as:
Perimeter of Rectangle=2(l+b)=4s
- This means:
l+b=2s
- The area of the rectangle is given by:
Area of Rectangle=l×b
4. Conclusion:
- From the above calculations, we can conclude that when the wire is re-bent into a rectangle, the perimeter of both shapes (the square and the rectangle) remains the same.
- However, the area of the two shapes may vary depending on the dimensions of the rectangle chosen.
Final Answer:
If a wire in the shape of a square is rebent into a rectangle, then the perimeter of both shapes remains the same, but area may vary.
- We start with a wire shaped like a square. Let's denote the length of one side of the square as s.
- The perimeter of a square is given by the formula:
Perimeter of Square=4s
- When the wire is re-bent into a rectangle, it will still have the same length as the perimeter of the square.
- Therefore, the perimeter of the rectangle will also be:
Perimeter of Rectangle=4s
- The area of the square can be calculated using the formula:
Area of Square=s2
- For the rectangle, let’s denote the length as l and the breadth as b. The perimeter of the rectangle can be expressed as:
Perimeter of Rectangle=2(l+b)=4s
- This means:
l+b=2s
- The area of the rectangle is given by:
Area of Rectangle=l×b
- From the above calculations, we can conclude that when the wire is re-bent into a rectangle, the perimeter of both shapes (the square and the rectangle) remains the same.
- However, the area of the two shapes may vary depending on the dimensions of the rectangle chosen.
If a wire in the shape of a square is rebent into a rectangle, then the perimeter of both shapes remains the same, but area may vary.
Topper's Solved these Questions
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Exercise (True or false)
7 Videos
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Think and Discuss
7 Videos
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Exercise
96 Videos
- LINES AND ANGLES BOOK - NCERT EXEMPLARCHAPTER - LINES AND ANGLES EXERCISE - Exercise (fill in the blanks)
3 Videos
- PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESBOOK - NCERT EXEMPLARCHAPTER - PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESEXERCISE - EXERCISE
108 Videos
Similar Questions
Knowledge Check
The shape of water molecule is same as that of
AC2H2BCO2CNH3DCl2OThe shape of water molecule is same as that of
AC2H2BCO2CNH3DCl2OIf the wire in the shape of square of perimeter 44 cm is turned into a circle with same circumference, then find the area of the circle formed.
A77cm2B308cm2C154cm2D231cm2
A wire is in the shape of a square of side 10 cm. If the wire is rebent into a rectangle of length 12 cm, find its breadth. Which figure encloses more area and by how much?
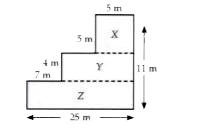
View SolutionThe given shape is divided into a square and two rectangles.
What is the area of the given shape ?
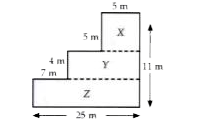
View SolutionThe given shape is divided into a square and two rectangles.
What is the area of square X ?
View SolutionIf a wire is bent into the shape of a square, then the area of the square is 81 sq. cm. When the wire is bent into a semi-circular shape, then the area of the semi-circle will be (a) 22 cm2 (b) 44 cm2 (c) 77 cm2 (d) 154 cm2
View SolutionIf a wire is bent into the shape of a square, then the area of the square so formed is 81cm2 . When the wire is rebent into a semicircular shape, then the area, (in cm2) of the semicircle will be
View Solution
