If a1,a2,a3,……a87,a88,a89 are the arithmetic means between 1 and 89, then 89∑r=1log(tan(ar)∘) is equal to
0
1
log23
log5
The correct Answer is:A
To solve the problem step by step, we will follow the reasoning provided in the video transcript and break it down into clear steps.
1. Understanding the Arithmetic Means:
We have a1,a2,a3,…,a89 as the arithmetic means between 1 and 89. This means:
ar=1+(r)(89−1)90for r=1,2,…,89
2. Expression for the Summation:
We need to evaluate:
89∑r=1log(tan(ar))
This can be rewritten using the property of logarithms:
=log(89∏r=1tan(ar))
3. Using the Property of Arithmetic Means:
Since ar are arithmetic means, we know that:
ar+a90−r=90for r=1,2,…,44
This implies:
a90−r=90−ar
4. Using the Tangent Identity:
From the tangent identity:
tan(90−x)=cot(x)
We can express:
tan(a90−r)=tan(90−ar)=cot(ar)
5. Pairing the Terms:
The product of terms can be paired:
tan(ar)tan(a90−r)=tan(ar)cot(ar)=1
Thus, for r=1 to 44:
44∏r=1tan(ar)tan(a90−r)=1
6. Considering the Middle Term:
The middle term a45 is:
a45+a45=90⟹2a45=90⟹a45=45
Therefore:
tan(a45)=tan(45)=1
7. Final Calculation:
Now substituting back into the logarithmic expression:
89∏r=1tan(ar)=1(from pairs)andtan(a45)=1
Thus:
log(89∏r=1tan(ar))=log(1)=0
Conclusion:
The value of the summation 89∑r=1log(tan(ar)) is:
0
We have a1,a2,a3,…,a89 as the arithmetic means between 1 and 89. This means:
ar=1+(r)(89−1)90for r=1,2,…,89
We need to evaluate:
89∑r=1log(tan(ar))
This can be rewritten using the property of logarithms:
=log(89∏r=1tan(ar))
Since ar are arithmetic means, we know that:
ar+a90−r=90for r=1,2,…,44
This implies:
a90−r=90−ar
From the tangent identity:
tan(90−x)=cot(x)
We can express:
tan(a90−r)=tan(90−ar)=cot(ar)
The product of terms can be paired:
tan(ar)tan(a90−r)=tan(ar)cot(ar)=1
Thus, for r=1 to 44:
44∏r=1tan(ar)tan(a90−r)=1
The middle term a45 is:
a45+a45=90⟹2a45=90⟹a45=45
Therefore:
tan(a45)=tan(45)=1
Now substituting back into the logarithmic expression:
89∏r=1tan(ar)=1(from pairs)andtan(a45)=1
Thus:
log(89∏r=1tan(ar))=log(1)=0
The value of the summation 89∑r=1log(tan(ar)) is:
0
Topper's Solved these Questions
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - EXERCIESE ( MULTIPLE CORRECT ANSWER TYPE )
66 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - EXERCIESE ( MATRIX MATCH TYPE )
3 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )
8 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
Similar Questions
If a1,a2,a3,…an+1 are in arithmetic progression, then n∑k=0.nCk.ak+1 is equal to (a)2n(a1+an+1) (b)2n−1(a1+an+1) (c)2n+1(a1+an+1) (d)(a1+an+1)
View SolutionIf a1,a2,a3,a4 and a5 are in AP with common difference ≠0, find the value of 5∑i=1ai when a3=2.
View SolutionIf a1,a2,a3,…. are in A.P., then ap,aq,ar are in A.P. if p,q,r are in
View SolutionIf A1,A2 are between two numbers, then A1+A2H1+H2 is equal to
View SolutionIf A1,A2,A3,....A51 are arithmetic means inserted between the number a and b, then find the value of (b+A51b−A51)−(A1+aA1−a)
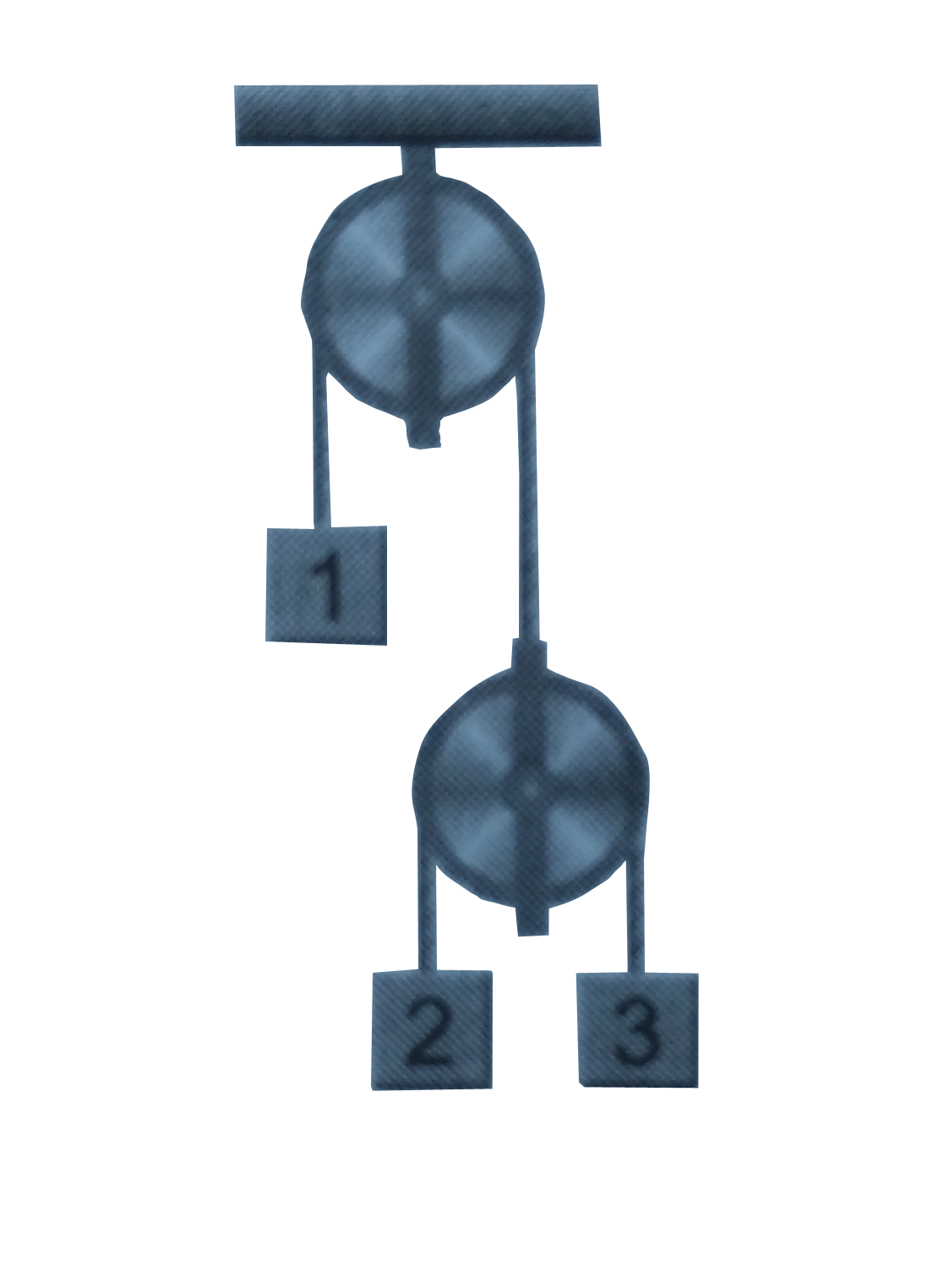
View SolutionMake the constraint relation between a1,a2 and a3
View SolutionFor an increasing G.P. a1,a2,a3,.....an, If a6=4a4,a9−a7=192, then the value of ∞∑l=11ai is
View SolutionStatement-1: If f:{a1,a2,a3,a4,a5}→{a1,a2,a3,a4,a5}, f is onto and f(x)≠x for each x<br>∈{a1,a2,a3,a4,a5}, is equal to 44.
Statement-2: The number of derangement for n objects is
n!n∑r=0(−1)rr!.
View SolutionIf a1,a2,a3,a4,a5 are consecutive terms of an arithmetic progression with common difference 3, then the value of ∣∣ ∣ ∣∣a23a2a1a24a3a2a25a4a3∣∣ ∣ ∣∣ is
View SolutionIf a1,a2,a3,a4,,……,an−1,an are distinct non-zero real numbers such that (a21+a22+a23+…..+a2n−1)x2+2(a1a2+a2a3+a3a4+……+an−1an)x+(a22+a23+a24+......+a2n)≤0 then a1,a2,a3,.....,an−1,an are in
View Solution
