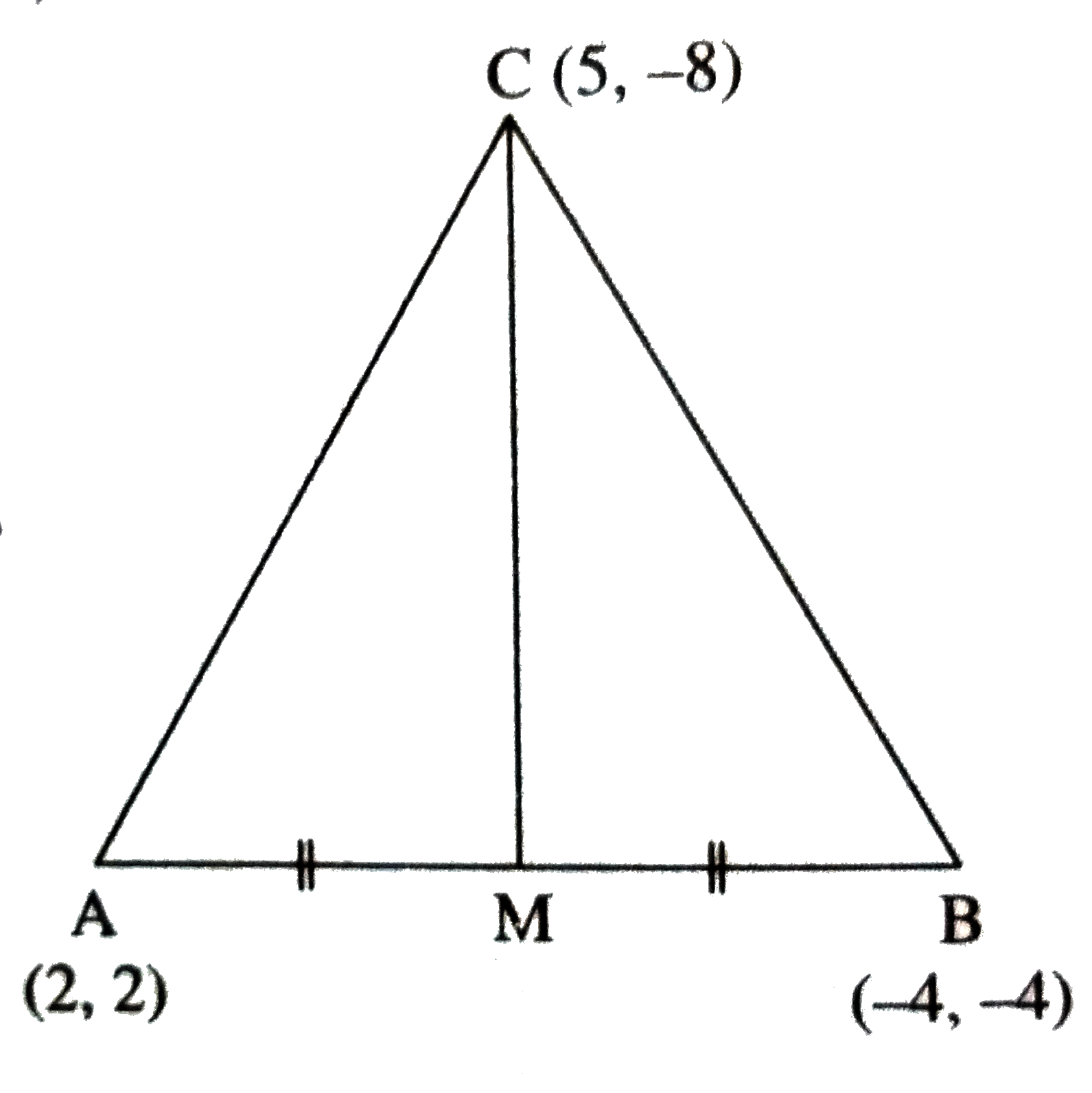
If A(2,2),B(−4,−4)andC(5,−8) are the vertices of a triangle, then the lengthof the median through vertex C is.
√65
√75
√85
None of these
The correct Answer is:C
By midpoint formula, M will have coordinates (-1, 1) Now by distance formula median CM=√85
Similar Questions
Knowledge Check
- Question 1 - Select One
If P( 2, 2), Q( -2, 4) and R( 3, 4) are the vertices of ΔPQR then the equation of the median through vertex R is ...
Ax + 3y + 9 = 0Bx - 3y + 9 = 0CX - 3 y - 9 = 0DX + 3 y - 9 = 0
If A(6,2),B(4,2)andC(6,4) are the vertices of ΔABC, then find the length of the median through C.
View SolutionIf A(−2,4),B(0,0) and C(4,2) are the vertices of ΔABC , find the length of the median through A .
View SolutionIf A(-1, 3), B(1, -1) and C(5, 1) are the vertices of triangle ABC, find the length of the median passing through the vertex through A.
View SolutionIf A(5,−1),B(−3,−2)and(−1,8) are the vertices of triangle ABC, find the length of median through A and the coordinates of the centroid.
View SolutionShow that A(6,4),B(5,−2)andC(7,−2) are the vertices of an isosceles triangle. Also, find the length of the median through A.
View SolutionIf A(-3,0),B(4,-1),C(5,2) are vertices of △ ABC, then the length of altitude through A is
View SolutionA(5, 4), B(-3, -2) and C(1,-8) are the vertices of a triangle ABC. Find the equation of median AD
View Solution

