If A=[3−5−4 2]. Find the value ofA2−5A−14I
The correct Answer is:0
To solve the problem, we need to find the value of A2−5A−14I where A=(3−5−42) and I is the identity matrix of the same order as A.
1. Calculate A2:
A2=A⋅A=(3−5−42)⋅(3−5−42)
To perform the multiplication:
- First row, first column: 3⋅3+(−5)⋅(−4)=9+20=29
- First row, second column: 3⋅(−5)+(−5)⋅2=−15−10=−25
- Second row, first column: −4⋅3+2⋅(−4)=−12−8=−20
- Second row, second column: −4⋅(−5)+2⋅2=20+4=24
Thus,
A2=(29−25−2024)
2. Calculate 5A:
5A=5⋅(3−5−42)=(15−25−2010)
3. Calculate 14I:
The identity matrix I for a 2×2 matrix is:
I=(1001)
Therefore,
14I=14⋅(1001)=(140014)
4. Combine the results to find A2−5A−14I:
A2−5A−14I=(29−25−2024)−(15−25−2010)−(140014)
Now, perform the subtraction step by step:
- First, calculate A2−5A:
A2−5A=(29−15−25−(−25)−20−(−20)24−10)=(140014)
- Now, subtract 14I:
A2−5A−14I=(140014)−(140014)=(0000)
5. Conclusion:
A2−5A−14I=(0000)
A2=A⋅A=(3−5−42)⋅(3−5−42)
To perform the multiplication:
- First row, first column: 3⋅3+(−5)⋅(−4)=9+20=29
- First row, second column: 3⋅(−5)+(−5)⋅2=−15−10=−25
- Second row, first column: −4⋅3+2⋅(−4)=−12−8=−20
- Second row, second column: −4⋅(−5)+2⋅2=20+4=24
A2=(29−25−2024)
5A=5⋅(3−5−42)=(15−25−2010)
The identity matrix I for a 2×2 matrix is:
I=(1001)
Therefore,
14I=14⋅(1001)=(140014)
A2−5A−14I=(29−25−2024)−(15−25−2010)−(140014)
Now, perform the subtraction step by step:
- First, calculate A2−5A:
A2−5A=(29−15−25−(−25)−20−(−20)24−10)=(140014)
- Now, subtract 14I:
A2−5A−14I=(140014)−(140014)=(0000)
A2−5A−14I=(0000)
Topper's Solved these Questions
- MATRICESBOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5A
9 Videos
- MATRICESBOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5B
16 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - SECTION D
6 Videos
- METHODS OF INTEGRATION BOOK - RS AGGARWALCHAPTER - METHODS OF INTEGRATION EXERCISE - Objective Questions Ii
56 Videos
Similar Questions
Find the values of (−i)25
View SolutionFind the value of |2+5i|
View SolutionFind the value of 5!+4!−3!−2!
View SolutionFind the value of {(2.5)−5}4 is -
View SolutionFind the value of (23)−4/5.
View SolutionFind the value of 2354
View SolutionIf A=[3−5−12] then find A2−5A−4I.
View SolutionFind the value of : (1−√3i)2/5.
View Solution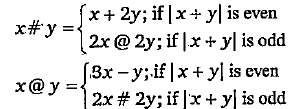
Find the value of 2#((7@(4#5)@3) :
View Solutionfind the value of |3+4i|+|1+5i|2
View Solution
