If α and 1α are the zeroes of the polynomial 4x2−2x+(k−4), then value of k is:
4
8
0
None of these
The correct Answer is:B
To find the value of k for the polynomial 4x2−2x+(k−4) given that α and 1α are its zeroes, we can follow these steps:
Step 1: Identify the coefficients of the polynomial
The polynomial is given as:
4x2−2x+(k−4)
Here, the coefficients are:
- a=4
- b=−2
- c=k−4
Step 2: Use the properties of the roots
For a quadratic polynomial ax2+bx+c, if α and β are the roots, then:
1. The sum of the roots α+β=−ba
2. The product of the roots α⋅β=ca
In our case, the roots are α and 1α.
Step 3: Calculate the sum of the roots
The sum of the roots is:
α+1α=−−24=24=12
Step 4: Calculate the product of the roots
The product of the roots is:
α⋅1α=1=k−44
Step 5: Set up the equation for the product of the roots
From the product of the roots, we have:
1=k−44
Step 6: Solve for k
To solve for k, multiply both sides by 4:
4=k−4
Now, add 4 to both sides:
k=4+4=8
Final Answer
The value of k is:
8
The polynomial is given as:
4x2−2x+(k−4)
Here, the coefficients are:
- a=4
- b=−2
- c=k−4
For a quadratic polynomial ax2+bx+c, if α and β are the roots, then:
1. The sum of the roots α+β=−ba
2. The product of the roots α⋅β=ca
The sum of the roots is:
α+1α=−−24=24=12
The product of the roots is:
α⋅1α=1=k−44
From the product of the roots, we have:
1=k−44
To solve for k, multiply both sides by 4:
4=k−4
Now, add 4 to both sides:
k=4+4=8
The value of k is:
8
Topper's Solved these Questions
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section - A
6 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section - B
5 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section -C
7 Videos
Similar Questions
If αand1α are the zeroes of the polnomial 4x2−2x+(k−4), find the value of k.
View SolutionIf α and β are the zeroes of the polynomial 2x2−4x+5 then match the value of List-I with that of List-II.
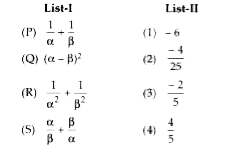
View SolutionIF αandβ are the zeroes of the polynomial p(x)=4x2−2x−3 find the value of 1α+1β
View SolutionIf α and β are the zeros of the quadratic polynomial f(x)=x2−x−4 , find the value of 1α+1β−αβ .
View SolutionIf α and β are the zeroes of the polynomial 2x2−4x+5 find the value of α²+β2.
View SolutionIf α,β,γ are the zeroes of the polynomial x3+2x2−4x+1, find the values of (i) ∑1α and (ii) ∑α2.
View SolutionIf α and β are the zeros of the quadratic polynomial p(x)=4x2−5x−1 , find the value of α2β+αβ2 .
View SolutionIf α and β are the zeros of the quadratic polynomial f(x)=x2+x−2, find the value of 1α−1β
View SolutionIf α and β be the zeroes of the polynomial p(x)=x2−5x+2, find the value of 1α+1β−3αβ.
View SolutionIf -4 is a zero of the polynomial x2−x−(2k+2), then find the value of k.
View Solution
