If are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction-cosines of the line are :
.
The correct Answer is:B
To find the direction cosines of a line that makes angles α, β, and γ with the positive directions of the x, y, and z axes respectively, we can follow these steps:
1. Understanding Direction Cosines:
- The direction cosines of a line are defined as the cosines of the angles that the line makes with the coordinate axes.
2. Identify the Angles:
- Let α be the angle between the line and the positive x-axis.
- Let β be the angle between the line and the positive y-axis.
- Let γ be the angle between the line and the positive z-axis.
3. Calculate the Direction Cosines:
- The direction cosine with respect to the x-axis is given by:
l=cosα
- The direction cosine with respect to the y-axis is given by:
m=cosβ
- The direction cosine with respect to the z-axis is given by:
n=cosγ
4. Final Representation:
- Therefore, the direction cosines of the line can be represented as:
(l,m,n)=(cosα,cosβ,cosγ)
Conclusion:
The direction cosines of the line are cosα,cosβ,cosγ.
- The direction cosines of a line are defined as the cosines of the angles that the line makes with the coordinate axes.
- Let α be the angle between the line and the positive x-axis.
- Let β be the angle between the line and the positive y-axis.
- Let γ be the angle between the line and the positive z-axis.
- The direction cosine with respect to the x-axis is given by:
l=cosα
- The direction cosine with respect to the y-axis is given by:
m=cosβ
- The direction cosine with respect to the z-axis is given by:
n=cosγ
- Therefore, the direction cosines of the line can be represented as:
(l,m,n)=(cosα,cosβ,cosγ)
The direction cosines of the line are cosα,cosβ,cosγ.
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - MODERN PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - OBJECTIVE TYPE QUESTIONS (B. FILL IN THE BLANKS)
10 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - MODERN PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - OBJECTIVE TYPE QUESTIONS (C. TRUE/FALSE QUESTIONS)
7 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - MODERN PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 11 (F) (LONG ANSWER TYPE QUESTIONS (II) )
13 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - CHAPTER TEST (1)
12 Videos
- VECTOR ALGEBRA BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - CHAPTER TEST 10
12 Videos
Similar Questions
If a line makes angle 90∘, 60∘and 30∘with the positive direction of x, y and z-axis respectively, find its direction cosines.
View SolutionIf α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in
Column-I to their values in column-II :
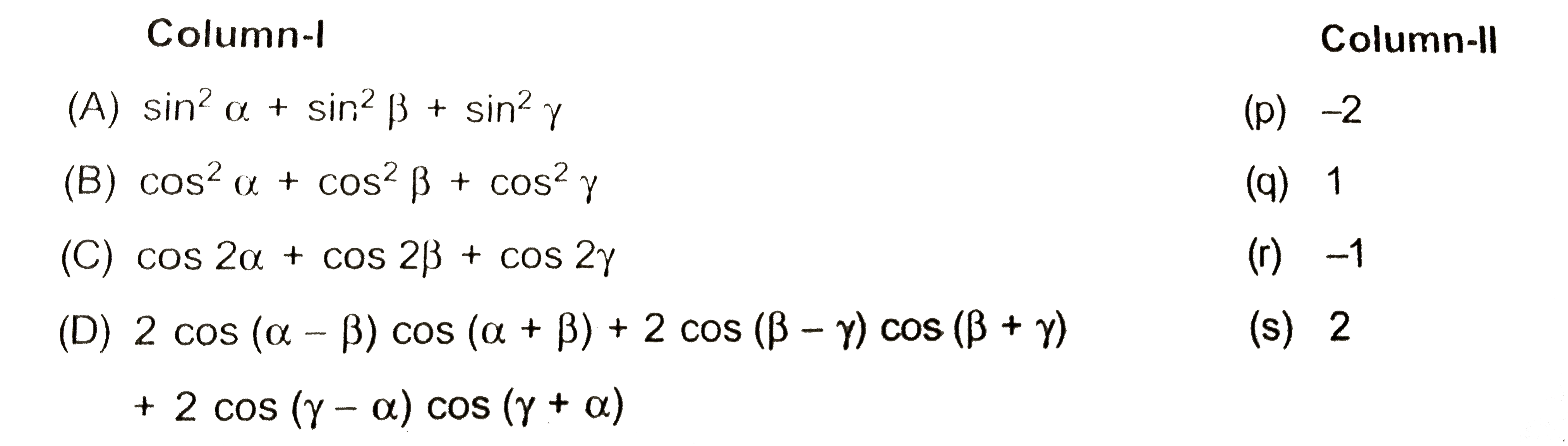
View Solution
Knowledge Check
If α,β,γ be the angles which a line makes with the coordinates axes, then
Asin2α+sin2β+sin2γ=1Bsin2α+sin2β+sin2γ=1Ccos2α+cos2β+cos2γ=1Dcos2α+sin2β+sin2γ=1If α,β,γ are direction angles of a line, then
A0≤α,β,γ≤π2B0≤α,β,γ≤πC0<α,β,γ<π2D0<α,β,γ<πThe direction cosines of the line x = y = z are
A1√3,1√3,1√3B13,13,13C1,1,1D2√3,2√3,2√3
Write the direction cosines of a line parallel to z-axis.
View SolutionIf α,β,γ be angles which a straighat line makes with the positive direction of the axes, then sin2α+sin2β+sin2γ is equal to (A) 4 (B) 1 (C) 2 (D) 3
View SolutionIf a line makes angles 60∘and45∘ with the Y and Z-axes respectively, then the direction cosines of the line are
View SolutionIf a line makes angles π2,3π4andπ4 with x,y,z axis respectively, then direction cosines of this line are :
View SolutionIf the line makes angles 45∘,60∘,120∘ with X, Y, Z axes respectively, then the direction consines of line are
View Solution
