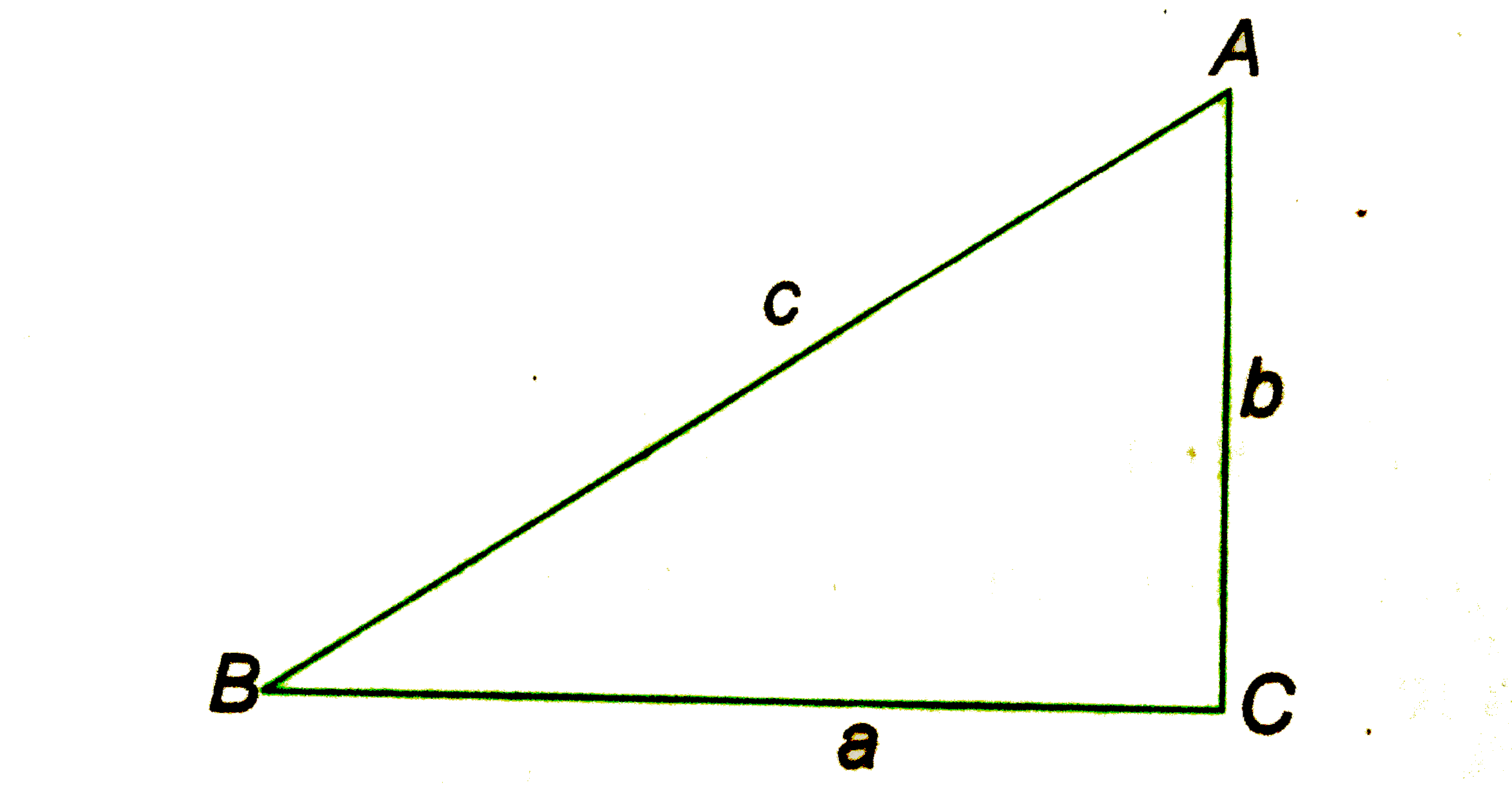
If angle C of triangle ABC is 900, then prove that tanA+tanB=c2ab (where, a,b,c, are sides opposite to angles A,B,C, respectively).
Video Solution
Text Solution
Draw ΔABC with ∠C=90∘. We have
tanA+tanB=ab+ba=a2+b2ab=c2ab
|
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.2
8 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.3
4 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
Knowledge Check
If angle C of triangle ABC is 900, then prove that tanA+tanB=c2ab (where, a,b,c, are sides opposite to angles A,B,C, respectively).
Aa2bcBb2caCc2abDa+bIf the angles A, B and C of a triangle are in an arithmetic progression and if a, b and c denote the lengths of the sides opposite to A, B and C respectively, then the value of the expression acsin2C+casin2A is
A12B√32C1D√3Let ABC is be a fixed triangle and P be veriable point in the plane of triangle ABC. Suppose a,b,c are lengths of sides BC,CA,AB opposite to angles A,B,C, respectively. If a(PA)2+b(PB)2+c(PC)2 is minimum, then point P with respect to ΔABC is
AcentroidBcircumcentreCorthocenterDincentre
In a triangle ABC,∠C=π2. If tan(A2) and tan(B2) are the roots of the equation ax2+bx+c=0,(a≠0), then the value of a+bc (where a,b,c, are sides of opposite to angles A,B,C, respectively) is
View SolutionUsing vectro mehod, prove that in a △ABC,asinA,bsinB=csinC where a,b,c are the lenths of the sides opposite to the angles A,B and C respectively of △ABC.
View SolutionIn △ABC, if ∠C=π2 , then prove sin(A−B)=a2−b2a2+b2.
View SolutionIn a ΔABC, if ∠C=90∘ , prove that sin2A+sin2 B = 1.
View SolutionΔ=∣∣ ∣ ∣∣14sinBbcosA2a8sinA13a12sinAcosB∣∣ ∣ ∣∣ is (where a,b,c are the sides opposite to angles A,B,C respectively in a triangle)
View Solution
