If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is (a) 17√3 units (b) 36 units (c) 72 units (d) 48√3 units
To solve the problem, we need to find the perimeter of an equilateral triangle given that the area of the inscribed circle is 48π square units.
1. Understand the area of the circle:
The area of a circle is given by the formula:
Area=πr2
where r is the radius of the circle.
2. Set up the equation:
We know the area of the inscribed circle is 48π:
πr2=48π
Dividing both sides by π:
r2=48
3. Calculate the radius:
Taking the square root of both sides:
r=√48=4√3
4. Relate the radius to the side of the triangle:
For an equilateral triangle, the radius r of the inscribed circle is related to the side length a of the triangle by the formula:
r=a√36
Setting this equal to our calculated radius:
4√3=a√36
5. Solve for the side length a:
Multiply both sides by 6:
24√3=a√3
Dividing both sides by √3:
a=24
6. Calculate the perimeter of the triangle:
The perimeter P of an equilateral triangle is given by:
P=3a
Substituting the value of a:
P=3×24=72
Thus, the perimeter of the triangle is 72 units.
Final Answer:
The correct option is (c) 72 units.
The area of a circle is given by the formula:
Area=πr2
where r is the radius of the circle.
We know the area of the inscribed circle is 48π:
πr2=48π
Dividing both sides by π:
r2=48
Taking the square root of both sides:
r=√48=4√3
For an equilateral triangle, the radius r of the inscribed circle is related to the side length a of the triangle by the formula:
r=a√36
Setting this equal to our calculated radius:
4√3=a√36
Multiply both sides by 6:
24√3=a√3
Dividing both sides by √3:
a=24
The perimeter P of an equilateral triangle is given by:
P=3a
Substituting the value of a:
P=3×24=72
The correct option is (c) 72 units.
Topper's Solved these Questions
Similar Questions
If the area of an equilateral triangle is 16√3cm2, then the perimeter of the triangle is
View SolutionThe area of a circle inscribed in an equilateral triangle is 154 cm2 . Find the perimeter of the triangle. [Use π=22/7and √3=1.73]
View SolutionThe area of an equilateral triangle is 36√3 sq. cm. Find its perimeter.
View SolutionA rectangle is inscribed in an equilateral triangle of side length 2a units. The maximum area of this rectangle can be (a) √3a2 (b) √3a24 a2 (d) √3a22
View SolutionThe area enclosed by 2|x|+3|y|≤6 is (a)3 sq. units (b) 4 sq. units (c)12 sq. units (d) 24 sq. units
View Solutionthe distance between the points (3,−2) and (−3,2) is
a) √52 units
b) 4√10 units
c) 2√10 units
d) √40 unitsView SolutionIf the centroid of a triangle is (1, 4) and two of its vertices are (4, −3) and (−9, 7) , then the area of the triangle is 183 sq. units (b) 1832 sq. units (c) 366 sq. units (d) 1834 sq. units
View Solution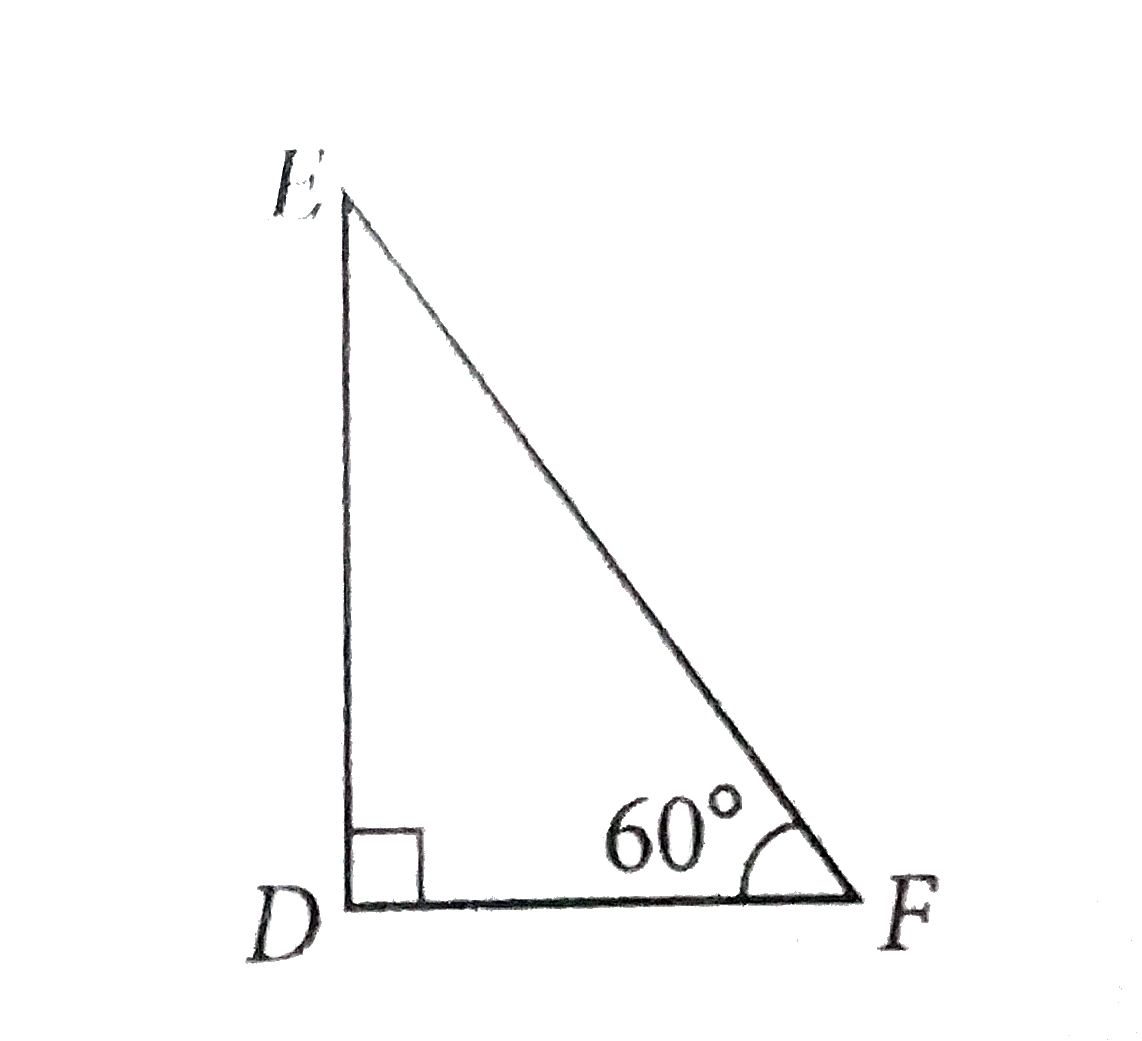
The area of triangle DEF is 32√3 square units. What is the length of ¯¯¯¯¯¯DF?View SolutionIn Fig. 3, the area of triangle ABC (in sq. units) is :
View SolutionOne angle of an isosceles triangle is 1200 and the radius of its incircle is √3. Then the area of the triangle in sq. units is
(a) 7+12√3 (b) 12−7√3 (c) 12+7√3 (d) 4πView Solution

