If A={x:|x|<2},B={x:|x−5|≤2},
C={x:|x|>x}andD={x:|x|<x}
The number of integral values in A∪C is
1
2
3
0
The correct Answer is:A
To solve the problem, we need to analyze the sets A and C and then find the number of integral values in the union of these sets.
Step 1: Define Set A
Set A is defined as:
A={x:|x|<2}
This means that x must be between -2 and 2, but not including -2 and 2. Therefore, we can express this as:
A=(−2,2)
Step 2: Identify Integral Values in Set A
The integral values in the interval (−2,2) are:
- −1
- 0
- 1
Thus, the integral values in set A are:
{−1,0,1}
Step 3: Define Set C
Set C is defined as:
C={x:|x|>x}
We need to analyze this condition. The expression |x|>x holds true for negative values of x because:
- If x is negative, |x|=−x and thus −x>x (which is true).
- If x is non-negative (i.e., x≥0), then |x|=x and x>x is false.
Therefore, set C consists of all negative numbers:
C=(−∞,0)
Step 4: Identify Integral Values in Set C
The integral values in set C (which includes all negative integers) are:
{−1,−2,−3,…}
However, since we are interested in the union with set A, we will focus on the integral values that are also in A.
Step 5: Find the Union of Sets A and C
Now we find the union of sets A and C:
A∪C={−1,0,1}∪(−∞,0)
This union includes all negative integers and the values from set A:
A∪C={−1,0,1}∪{−1,−2,−3,…}
Thus, the integral values in A∪C are:
{−1,−2,−3,…,0,1}
Step 6: Count the Integral Values
The integral values in A∪C are:
- All negative integers (which are infinite)
- 0
- 1
Since the negative integers are infinite, we conclude that the number of integral values in A∪C is infinite.
Final Answer
The number of integral values in A∪C is infinite.
---
Set A is defined as:
A={x:|x|<2}
This means that x must be between -2 and 2, but not including -2 and 2. Therefore, we can express this as:
A=(−2,2)
The integral values in the interval (−2,2) are:
- −1
- 0
- 1
{−1,0,1}
Set C is defined as:
C={x:|x|>x}
We need to analyze this condition. The expression |x|>x holds true for negative values of x because:
- If x is negative, |x|=−x and thus −x>x (which is true).
- If x is non-negative (i.e., x≥0), then |x|=x and x>x is false.
C=(−∞,0)
The integral values in set C (which includes all negative integers) are:
{−1,−2,−3,…}
However, since we are interested in the union with set A, we will focus on the integral values that are also in A.
Now we find the union of sets A and C:
A∪C={−1,0,1}∪(−∞,0)
This union includes all negative integers and the values from set A:
A∪C={−1,0,1}∪{−1,−2,−3,…}
Thus, the integral values in A∪C are:
{−1,−2,−3,…,0,1}
The integral values in A∪C are:
- All negative integers (which are infinite)
- 0
- 1
The number of integral values in A∪C is infinite.
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 1
11 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 2
10 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
17 Videos
Similar Questions
Knowledge Check
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A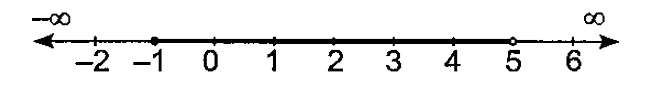 B
B C
C D
D
The number of integral solutions of x2−3x−4<0, is
View SolutionThe number of intergal values of x if 5x−1<(x+1)2<7x−3 is
View SolutionThe number of integral value of x satistying √x2+10x−16<x−2 is
View SolutionC={x:x is a composite number and 5≤x≤21}
View SolutionGiven A={x:−1<x≤5,x∈R}andB={x:−4≤x<3,x∈R}.
Represent on different number line :
A - B
View SolutionThe value of integral ∫ba|x|xdx, a<b is :
View SolutionGiven A={x:−1<x≤5,x∈R}andB={x:−4≤x<3,x∈R}.
Represent on different number line :
A'∩B
View Solution
