If cosA is not is Quadrant I, what is the value of ?
The correct Answer is:A
To find the value of sinA given that cosA=45 and angle A is not in Quadrant I, we can follow these steps:
Step 1: Use the Pythagorean Identity
We know from the Pythagorean identity that:
sin2A+cos2A=1
This means we can express sin2A in terms of cos2A:
sin2A=1−cos2A
Step 2: Calculate cos2A
Given cosA=45, we can calculate cos2A:
cos2A=(45)2=1625
Step 3: Substitute cos2A into the Identity
Now we substitute cos2A into the Pythagorean identity:
sin2A=1−1625
Step 4: Simplify the Expression
We need to simplify the right-hand side:
sin2A=2525−1625=925
Step 5: Take the Square Root
Now we take the square root of both sides to find sinA:
sinA=±√925=±35
Step 6: Determine the Sign of sinA
Since we know that angle A is not in Quadrant I, it must be in either Quadrant II or Quadrant III. In these quadrants, the sine function is negative in Quadrant III and positive in Quadrant II. Since we are given that A is not in Quadrant I, we need to determine which quadrant it is in.
If A is in Quadrant II, sinA would be positive, and if A is in Quadrant III, sinA would be negative. Since the problem does not specify, but implies that it is not in Quadrant I, we will assume it is in Quadrant III for this case.
Thus, we take the negative value:
sinA=−35
Final Answer
sinA=−35
---
We know from the Pythagorean identity that:
sin2A+cos2A=1
This means we can express sin2A in terms of cos2A:
sin2A=1−cos2A
Given cosA=45, we can calculate cos2A:
cos2A=(45)2=1625
Now we substitute cos2A into the Pythagorean identity:
sin2A=1−1625
We need to simplify the right-hand side:
sin2A=2525−1625=925
Now we take the square root of both sides to find sinA:
sinA=±√925=±35
Since we know that angle A is not in Quadrant I, it must be in either Quadrant II or Quadrant III. In these quadrants, the sine function is negative in Quadrant III and positive in Quadrant II. Since we are given that A is not in Quadrant I, we need to determine which quadrant it is in.
sinA=−35
sinA=−35
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
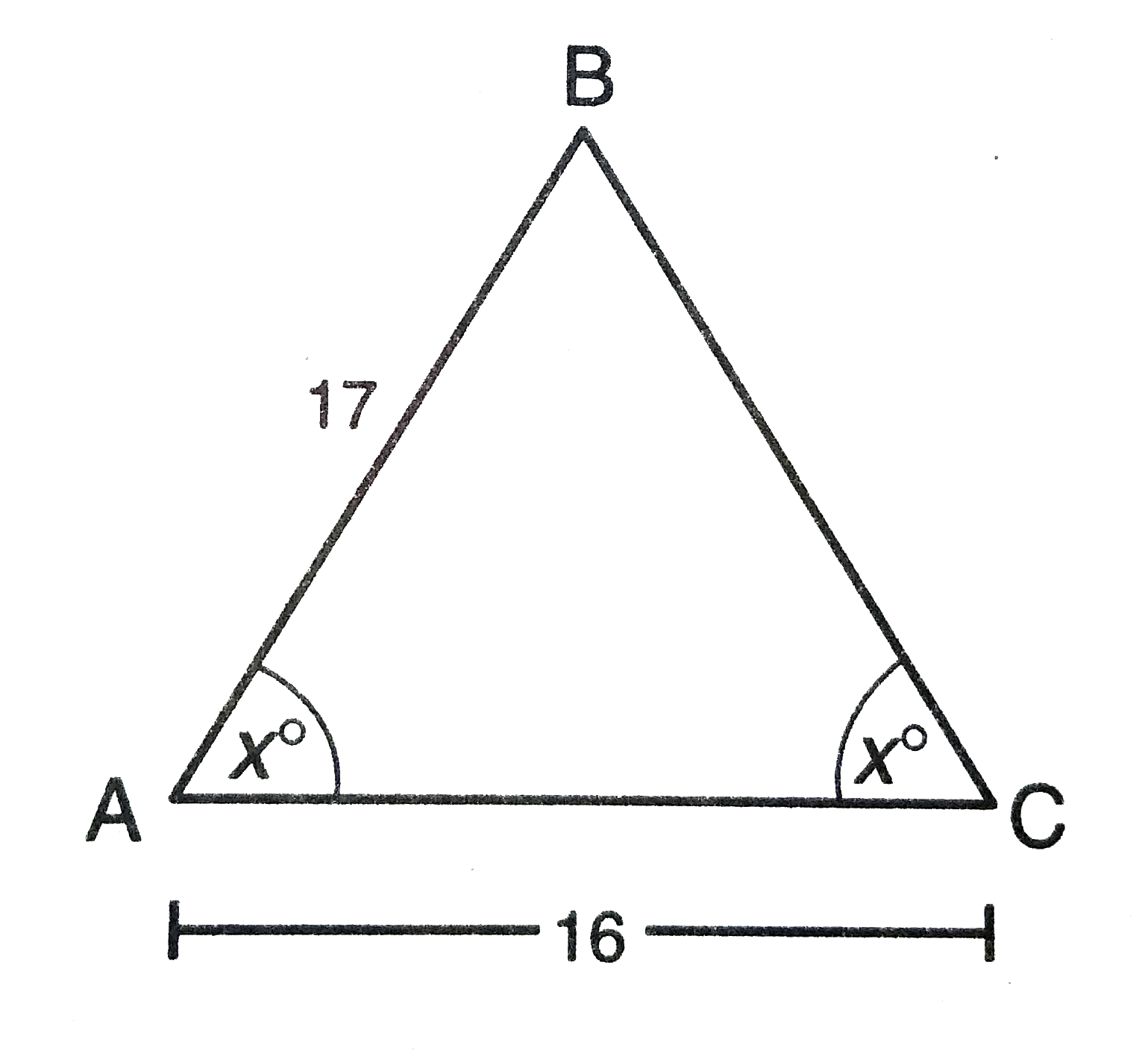
In the figure above, what is the value of sinA−cosA?
View SolutionIf sinA+cosA=0 and A lies in 4th quadrant, find the values of sinA and cosA.
View SolutionIf sinA=−45 and A lies in 3rd quadrant, find the values of (i) sin2A ii) cos2A.
View SolutionIf sinA=35 and cosB=−1215, where A and B both lie in second quadrant, then find the value of sin(A+B).
View SolutionIf sinA=cosA,then find the value of sin 2A.
View SolutionIf A lies in the second quadrant and 3tanA+4=0, then find the value of 2cotA−5cosA+sinA.
View SolutionIf tanA=512, find the value of (sinA+cosA)secA .
View SolutionIf cosA=0.6, find the value of 5sinA−3tanA.
View SolutioncosA1−sinA =
View SolutionIf cosA=513 and A lies in fourth quadrant, find the remaining trignometric ratios.
View Solution
