If cosecθ−cotθ=q, then the value of cosecθ is
q+1q
q−1q
12(q+1q)
None of these
The correct Answer is:C
To solve the equation cscθ−cotθ=q for cscθ, we can follow these steps:
Step 1: Write down the given equation
We start with the equation provided in the question:
cscθ−cotθ=q
Step 2: Use the trigonometric identity
We know from trigonometric identities that:
csc2θ−cot2θ=1
This can be factored as:
(cscθ−cotθ)(cscθ+cotθ)=1
Step 3: Substitute the known value
From the given equation, we can substitute cscθ−cotθ with q:
q(cscθ+cotθ)=1
Step 4: Solve for cscθ+cotθ
Now, we can express cscθ+cotθ in terms of q:
cscθ+cotθ=1q
Step 5: Set up a system of equations
Now we have two equations:
1. cscθ−cotθ=q (Equation 1)
2. cscθ+cotθ=1q (Equation 2)
Step 6: Add the two equations
Adding Equation 1 and Equation 2:
(cscθ−cotθ)+(cscθ+cotθ)=q+1q
This simplifies to:
2cscθ=q+1q
Step 7: Solve for cscθ
Now, divide both sides by 2 to isolate cscθ:
cscθ=12(q+1q)
Final Answer
Thus, the value of cscθ is:
cscθ=12(q+1q)
---
We start with the equation provided in the question:
cscθ−cotθ=q
We know from trigonometric identities that:
csc2θ−cot2θ=1
This can be factored as:
(cscθ−cotθ)(cscθ+cotθ)=1
From the given equation, we can substitute cscθ−cotθ with q:
q(cscθ+cotθ)=1
Now, we can express cscθ+cotθ in terms of q:
cscθ+cotθ=1q
Now we have two equations:
1. cscθ−cotθ=q (Equation 1)
2. cscθ+cotθ=1q (Equation 2)
Adding Equation 1 and Equation 2:
(cscθ−cotθ)+(cscθ+cotθ)=q+1q
This simplifies to:
2cscθ=q+1q
Now, divide both sides by 2 to isolate cscθ:
cscθ=12(q+1q)
Thus, the value of cscθ is:
cscθ=12(q+1q)
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Correct Answers Type
17 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Linked Comprehension Type
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.14
1 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
Knowledge Check
If cosecθ=53, then the value of tanθ+cotθ is
A11/25B12/25C25/11D25/12
If sinθ+cosθ=1, then the minimum value of (1+cosecθ)(1+secθ) is
View SolutionIf tan3θ=cotθ, then general value of θ is :
View SolutionIf 7(cosecθ−1)=3cotθ, shown that 3(cosecθ+1)=7cotθ.
View SolutionIf cosecθ+cotθ=p, then prove that the cosθ=p2−1p2+1
View Solution(a) the figure drawn alongside shows two straight lines AB and CD . if the equation of the line AB is x−√3y+5=0 and the equation of the line CD is x−y=2. write down the inclination of lines AB and CD; also find the angle θ i.e angle CPB
(b) if cosecθ.cos(θ+54∘)=1.find the value of θ so that θand(θ+54∘) are acute angles.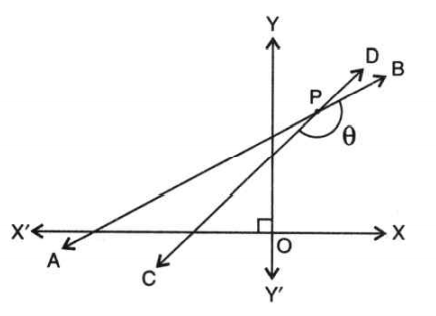
View SolutionIf cotθ=940 , find the values of cosec θ and secθ .
View SolutionIf cotθ=43, then find the value of sinθ,cosθ and cosec θ in first quadrant.
View Solution
