If D,E,F are the mid-points of the sides BC, Ca and AB respectively of a triangle ABC, prove by vector method that Area of $Δ D E F$ = 1/4 Area of $Δ A B C$

Video Solution

Text Solution

Verified by Experts

In $Δ A B C, D and F$ are the midpoints of sides AB and CA respectively.
$∴ D F ∣ ∣ B C$ [ by midpoint theorem]
$\Rightarrow D F ∣ ∣ B E$ .
Similarly, $E F ∣ ∣ B D$ .
$∴ B E F D$ is parallelogram

$\Rightarrow ∠ B = ∠ E F D, E F = B D = \frac{1}{2} A B$
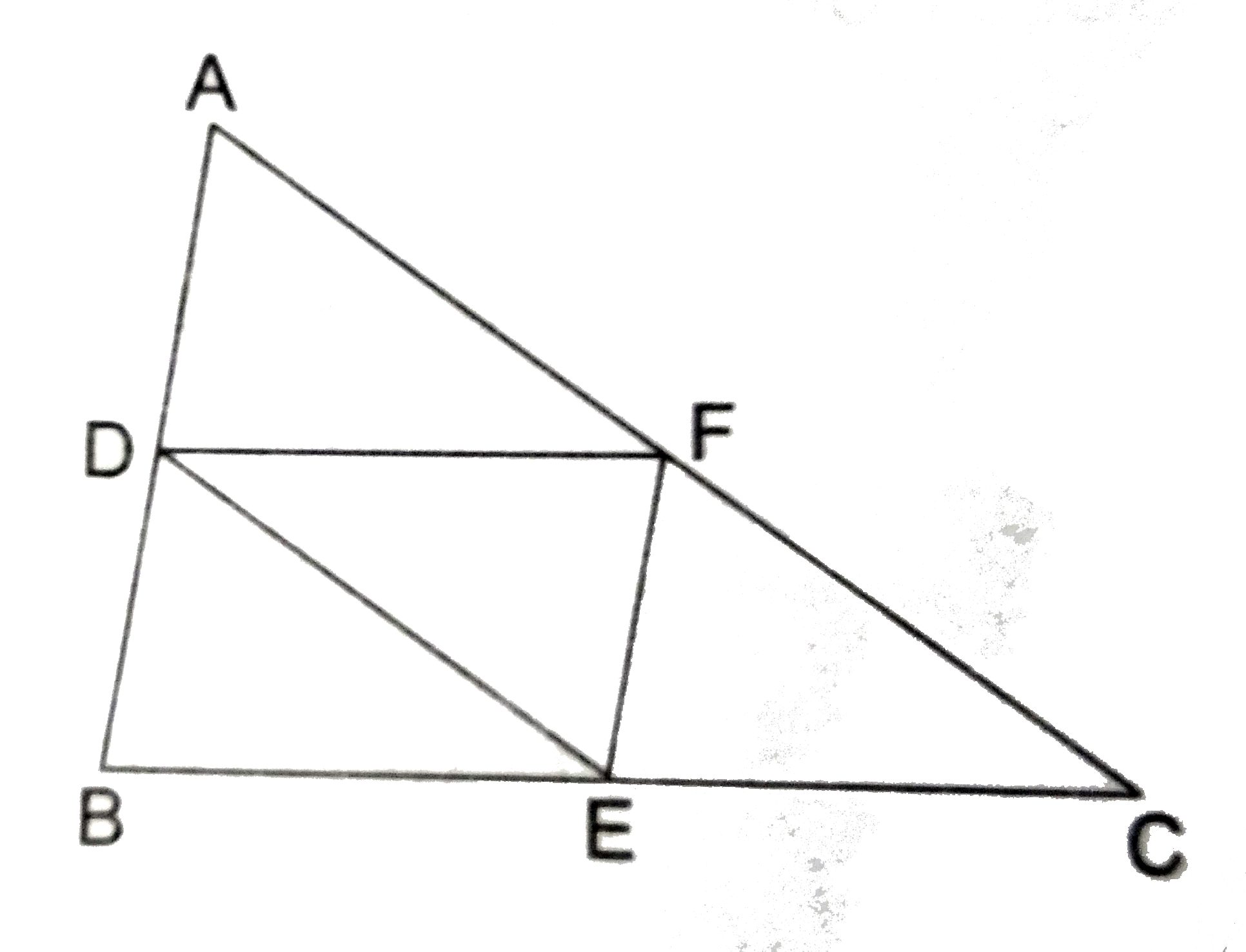
and $D F = B E = \frac{1}{2} B C$ .
Also, ECFD is parallelogram
$\Rightarrow ∠ E F D = ∠ B$
and $∠ E D F = ∠ C$
$∴ Δ D E F ~ Δ C A B$ [ by AA- similarity]
And so, $\frac{a r (Δ D E F)}{a r (Δ A B C)} = \frac{a r (Δ D E F)}{a r (Δ C A B)} = \frac{D F^{2}}{B C^{2}} = \frac{{(\frac{1}{2} B C)}^{2}}{B C^{2}} = \frac{1}{4}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If D, E and F are the mid-points of sides BC, CA and AB respectively of $△ A B C$ , then the ratio of the areas of $△ D E F$ to the area of $△ A B C$ is :
A $1 : 4$
B $1 : 2$
C $1 : 3$
D $2 : 3$
Question 2 - Select One
In a $Δ A B C, D, E, F$ are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A $- - \to B E + - - \to C F$
B $- - \to B E - - - \to C F$
C $- - \to C F - - - \to B E$
D $- - - \to B E - - - \to C F$
Question 3 - Select One
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0
B0
C2
DNone of these

RS AGGARWAL-TRIANGLES-Test Yourself

Home
Ask Doubt
Profile