If f is an even function, then find the realvalues of x satisfying the equation f(x)=f(x+1x+2)
The correct Answer is:x={−1+√52,−1−√52,−3+√52,−3−√52}
To solve the equation f(x)=f(x+1x+2) given that f is an even function, we can follow these steps:
Step 1: Use the property of even functions
Since f is an even function, we know that:
f(x)=f(−x)
This means that f(x)=f(x+1x+2) can also be expressed as:
f(x+1x+2)=f(−x+1x+2)
Step 2: Set up the equation
From the property of even functions, we can set up the following equation:
x=−x+1x+2
Step 3: Clear the fraction
To eliminate the fraction, we can multiply both sides by x+2:
x(x+2)=−(x+1)
This simplifies to:
x2+2x=−x−1
Step 4: Rearrange the equation
Rearranging gives us:
x2+2x+x+1=0
which simplifies to:
x2+3x+1=0
Step 5: Solve the quadratic equation
Now we can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=3,c=1:
x=−3±√32−4⋅1⋅12⋅1
This simplifies to:
x=−3±√9−42
x=−3±√52
Step 6: Find the solutions
Thus, the solutions for x are:
x=−3+√52andx=−3−√52
Final Answer
The real values of x satisfying the equation f(x)=f(x+1x+2) are:
x=−3+√52andx=−3−√52
Since f is an even function, we know that:
f(x)=f(−x)
This means that f(x)=f(x+1x+2) can also be expressed as:
f(x+1x+2)=f(−x+1x+2)
From the property of even functions, we can set up the following equation:
x=−x+1x+2
To eliminate the fraction, we can multiply both sides by x+2:
x(x+2)=−(x+1)
This simplifies to:
x2+2x=−x−1
Rearranging gives us:
x2+2x+x+1=0
which simplifies to:
x2+3x+1=0
Now we can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=3,c=1:
x=−3±√32−4⋅1⋅12⋅1
This simplifies to:
x=−3±√9−42
x=−3±√52
Thus, the solutions for x are:
x=−3+√52andx=−3−√52
The real values of x satisfying the equation f(x)=f(x+1x+2) are:
x=−3+√52andx=−3−√52
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 1
5 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 2
6 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
If f is symmetrical about x = 1, find the real values of x satisfying the equation f(x)=f(x+1x+2).
View SolutionIf f(x)=x2−3x+4, then find the values of x satisfying the equation f(x)=f(2x+1).
View SolutionIf f is an even function defined on the interval (−5,5), then four real values of x satisfying the equation f(x)=f(x+1x+2) are ______, __________, _______ and______.
View SolutionIf f(x) is an even function then find the number of distinct real numbers x such that f(x)=f(x+1x+2).
View SolutionIf f(x)=x2 is a real function, find the value of f(1).
View SolutionThe function f(x) satisfying the equation f2(x)+4f'(x)f(x)+(f'(x))2=0
View SolutionGiven f(x) is symmetrical about the line x=1, then find out the value of 'x' satisfying f(x−1)=f(xx+1)
View SolutionFind the period of the real-valued function satisfying f(x)+f(x+4)=f(x+2)+f(x+6).
View SolutionLet f:R−{0}→R be a function which is differentiable in its domain and satisfying the equation f(x+y)=f(x)+f(y)+x+yxy−1x+y, also f'(1)=2. Then find the function.
View SolutionThe graph of the function y=f(x) is shown.
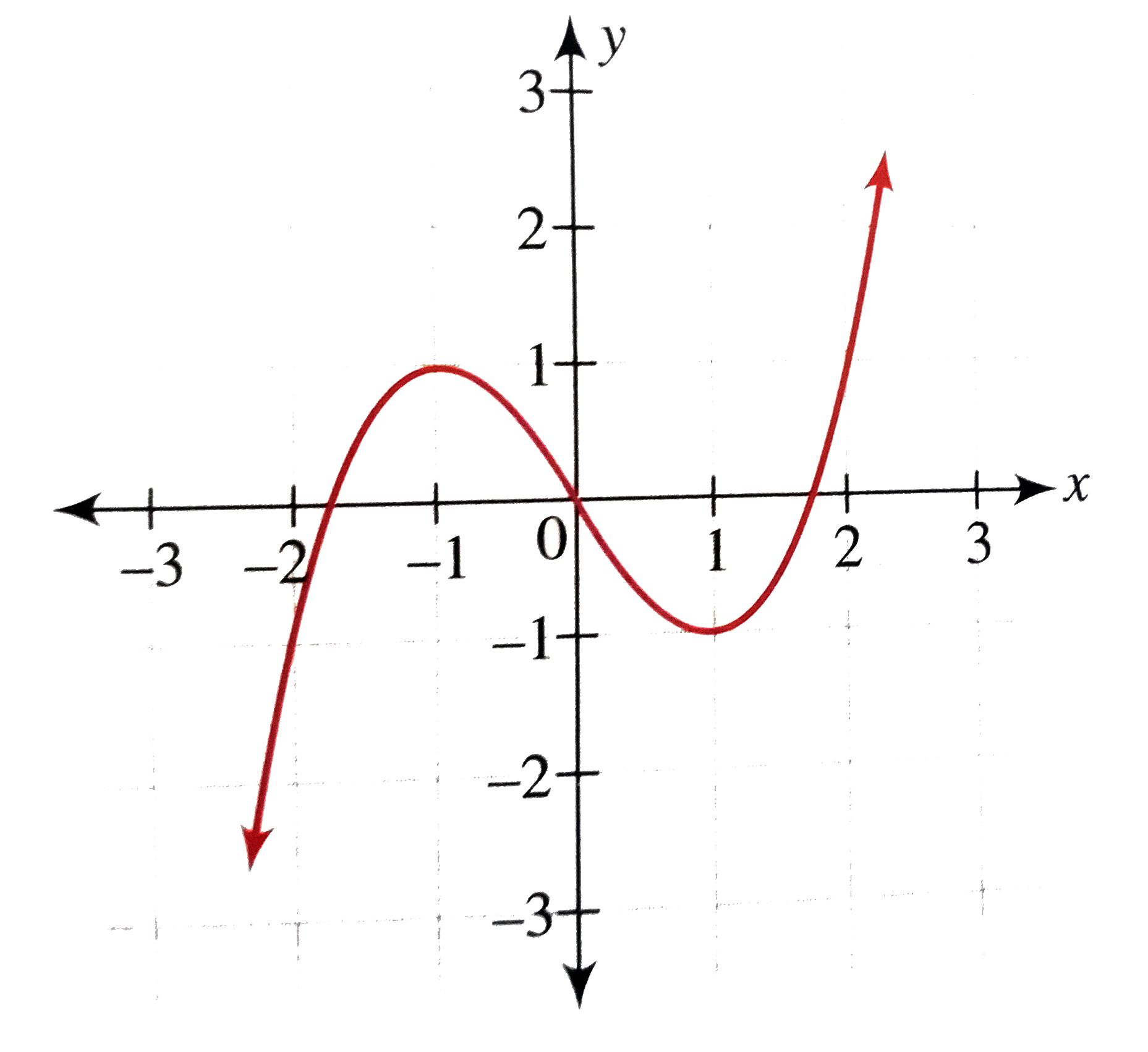
Find the number of solutions to the equation ||f(x)|−1|=12.
View Solution
