Question

If $f:R\to N\cup \left\{0\right\},$
where $f$
(area of triangle joining points $P(5,0),Q(8,4)andR(x,y)$
such that angle PRQ is a right angle) $=$
number of triangles, then which of the following is true?
(a) $f\left(5\right)=4$
(b) $f\left(7\right)=0$

(c) $f(6.25)=2$
(d) $f\left(x\right)$ is into

Answer

A::B::C::D

Explanation

Hence` angle PRQ=pi//2` and points P, Q, R lie on the circle with PQ as diameter.
Also, `PQ=5.`

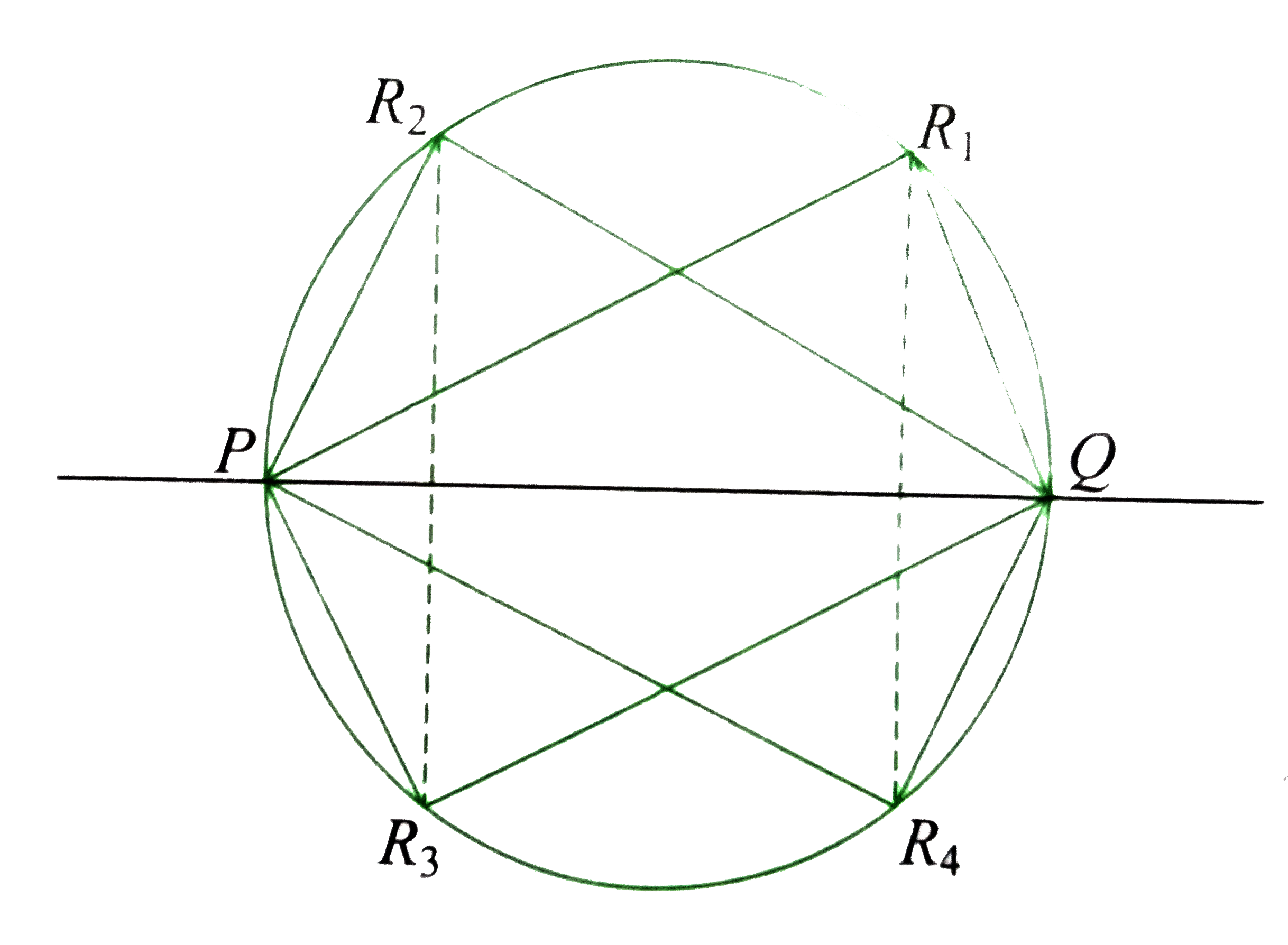
Now, the maximum area of the triangle is
`Delta_(max)=(1)/(2)(5)((5)/(2))=6.25`
For area = 5, we have four symmetrical positions of point R (shown as `R_(1), R_(2),R_(3), R_(4)`).
For area = 6.25, we have exactly two points.
For area = 7, no such points exist.