If f:R→N∪{0}, where f (area of triangle joining points P(5,0),Q(8,4)andR(x,y) such that angle PRQ is a right angle = number of triangles, then which of the following is true? f(5)=4 (b) f(7)=0 f(6,25)=2 (d) f(x)is¬
f(5)=4
f(7)=0
f(6.25)=2
f(4.5)=4
The correct Answer is:A, B, C, D
Hence∠PRQ=π/2 and points P, Q, R lie on the circle with PQ as diameter.
Also, PQ=5.
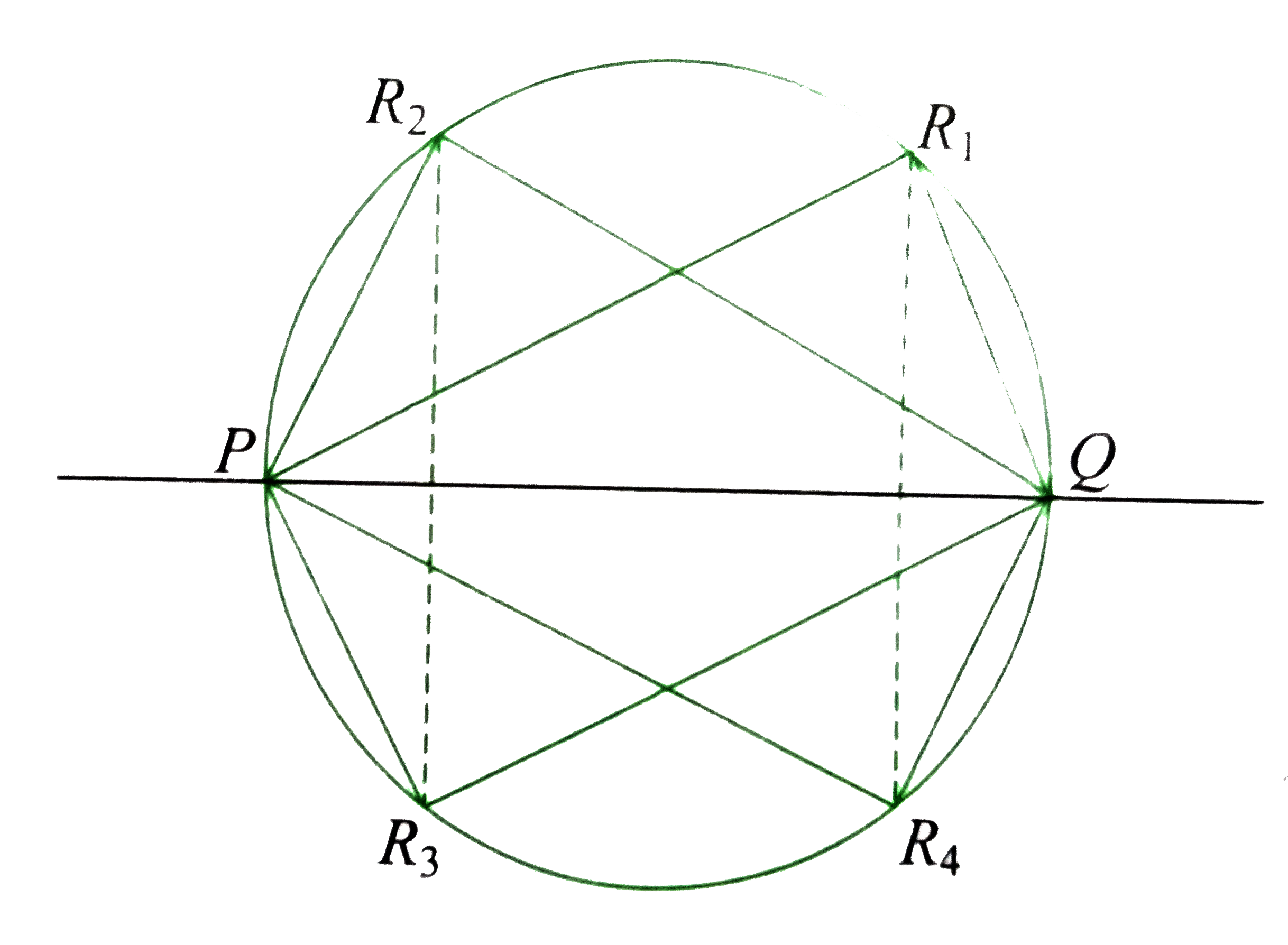
Now, the maximum area of the triangle is
Δmax=12(5)(52)=6.25
For area = 5, we have four symmetrical positions of point R (shown as R1,R2,R3,R4).
For area = 6.25, we have exactly two points.
For area = 7, no such points exist.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Single)
125 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
If f:R→N∪{0}, where f (area of triangle joining points P(5,0),Q(8,4)andR(x,y) such that angle PRQ is a right angle = number of triangles, then which of the following is true? f(5)=4 (b) f(7)=0 f(6,25)=2 (d) f(x)is¬
View SolutionIf f(x)=2x-5 , then evaluate the following:
(i) f(0)
(ii) f(7)
(iii) f(−3)
View Solution
Knowledge Check
Consider the non-constant differentiable function f of one variable which obeys the relation f(x)f(y)=f(x−y).Iff'(0)=pandf'(5)=q, then f'(−5) is
Ap2qBqpCpqDq
Consider f(x)=xx−1, which of the following statements is/are correct?
(A) f'(0)=−1
(B) f'(2)=−4
(C) f'(3)=−8
(D) f'(4)=−3
View SolutionIf graph of y=f(x) is symmetrical about the point (5,0) and f′(7)=3, then the value of f′(3) is__________
View SolutionFind the angle between y=f(x)andy=2e2x at their point of intersection. Where f(x)=x2f(1)−xf'(2)+f''(3) and f(0)=2.
View SolutionIf f(x)=tanx and A,B,C are the angles of △ABC, then ∣∣ ∣ ∣ ∣ ∣∣f(A)f(π4)f(π4)f(π4)f(B)f(π4)f(π4)f(π4)f(C)∣∣ ∣ ∣ ∣ ∣∣=
View SolutionFind the anti derivative F of f defined by f(x)=4x3−6, where F(0)=3
View SolutionGiven the function f(x) = 2x + 7. Find f(0), f(5), f(7).
View SolutionLet f(x) is a differentiable function on x∈R, such that f(x+y)=f(x)f(y) for all x,y∈R where f(0)≠0. If f(5)=10,f'(0)=0, then the value of f'(5) is equal to
View Solution
