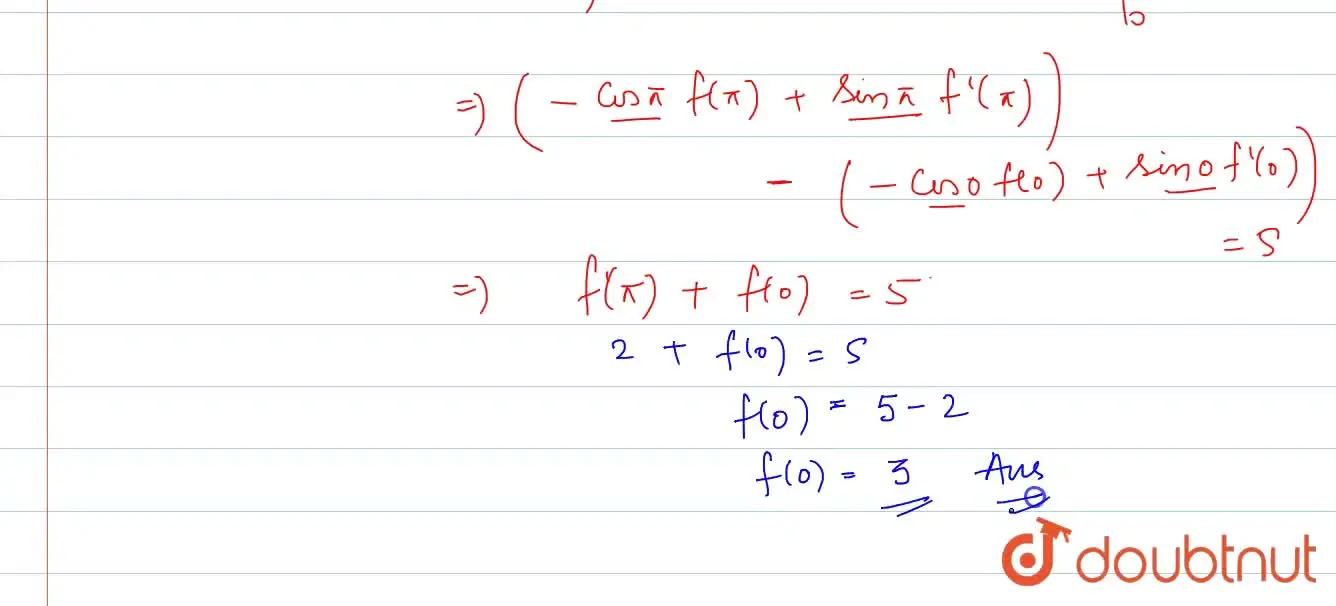If f(π)=2 and ∫π0(f(x)+f''(x))sinxdx=5, then f(0) is equal to ( it is given that f(x) is continuous in [0,π])
A
7
B
3
C
5
D
1
Video Solution
Text Solution
The correct Answer is:B
∫π0[f(x)+f''(x)]sinxdx
=∫π0f(x)sinxdx+∫π0f''(x)sinxdx
=(f(x)(−cosx))π0+∫π0f'(x)cosxdx
+sinxf'(x)∣π0−∫π0cosxf'(x)dx
=f(π)+f(0)=5 (given)
∴f(0)=5−f(π)=5−2=3
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - DEFINITE INTEGRATION EXERCISE - Exercise (Multiple)27videos
DEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - DEFINITE INTEGRATION EXERCISE - Exercise (Comprehension)31videos
DEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - DEFINITE INTEGRATION EXERCISE - Exercise 8.116videos
DEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - CURVE TRACINGEXERCISE - Exercise24videos
CURVE TRACING
- BOOK - CENGAGECHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer5videos
DETERMINANT
Similar Questions
If f(π)=2and∫π0(f(x)+f''(x))sinxdx=5 then f(0) is equal to
View SolutionIff(π)=2∫π0(f(x)+fx)sinxdx=5,thenf(0) is equal to (it is given that f(x) is continuous in [0,π]). 7 (b) 3 (c) 5 (d) 1
View Solution∫π0xf(sinx)dx=
View SolutionIf ∫π0xf(sinx)dx=A∫π/20f(sinx)dx, then A is equal to
View SolutionIf f(x)=∫x0sin4tdt, then f(x+2π) is equal to
View SolutionIf ∫π0xf(sinx)dx=a∫π0f(sinx)dx, then a =
View SolutionIf f'(x)=f(x)+∫10f(x) dx and given f(0)=1, then ∫f(x)dx is equal to :
View SolutionThe integral ∫π/20f(sin2x)sinxdx is equal to
View SolutionIf f(x)=f(π+e−x)and∫πef(x)dx=2e+π, then ∫πexf(x)dx is equal to
View SolutionIf ∫π0xf(sinx)dx=k∫π/20f(sinx)dx then the value of k is
View Solution