If from an extrenal point B of a circle with centre 0, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO i.e., BO=2BC.
Step by step video solution for If from an extrenal point B of a circle with centre 0, two tangents BC and BD are drawn such that angleDBC=120^(@), prove that BC+BD=BO i.e., BO=2BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.
 AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+AC
AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+AC
ABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
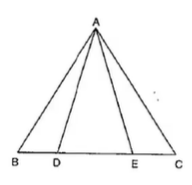
View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
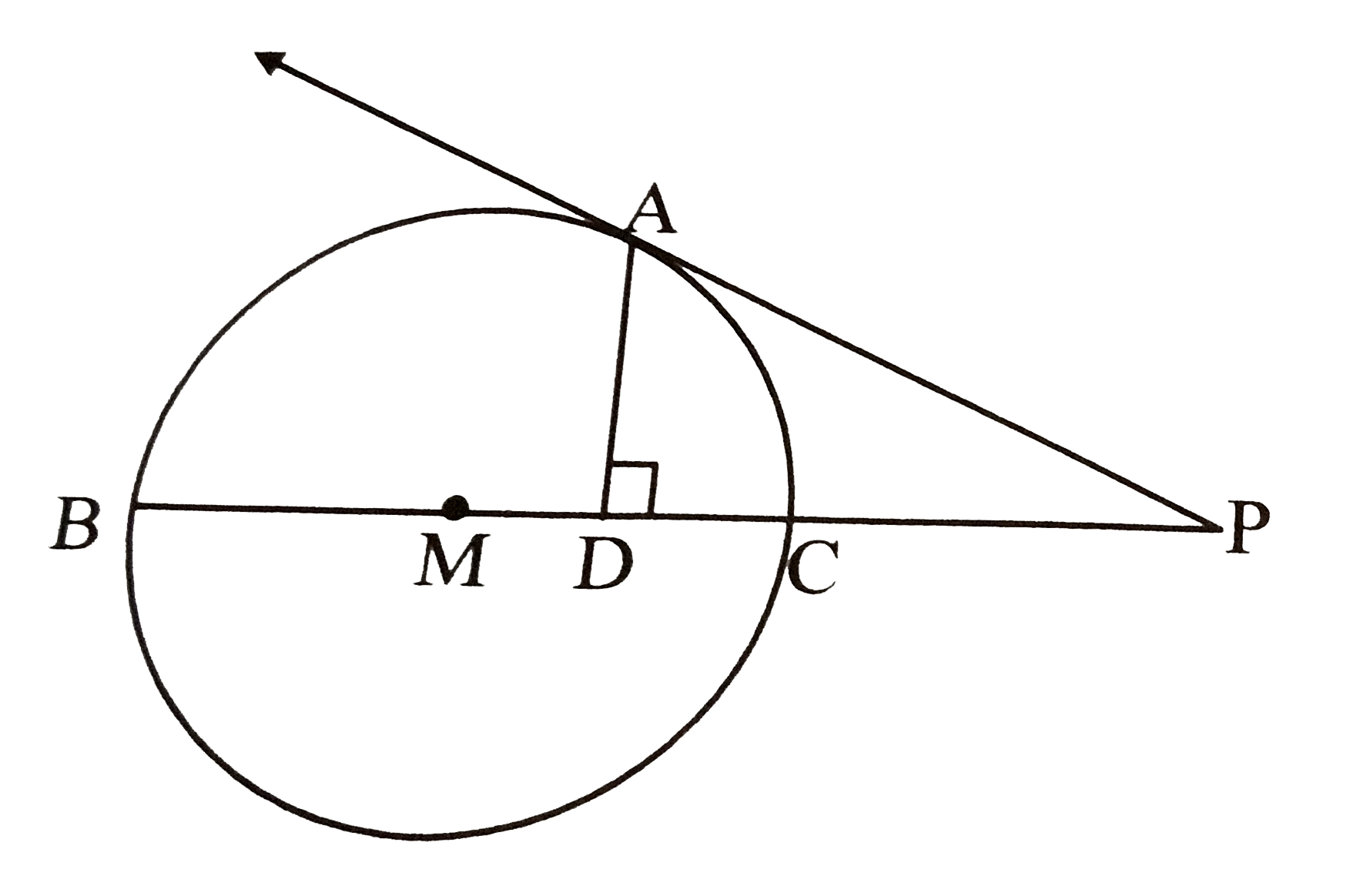
View SolutionIn the adjoining figure, BC is a diameter of the circle with centre M. PA is a tangent at A from P, which is a point on line BC. AD ⊥ BC
prove that DP2=BP×CP−BD×CD
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn △ABC, AB=AC and D is any point on BC, prove that AB2−AD2=BD.CD
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View Solution
