If f(x)=⎧⎪
⎪⎨⎪
⎪⎩ex,0≤x<12−ex−1,1<x≤2andg(x)=∫x0f(t)dt,x−e,2<x≤3
x∈[1,3], then
a. g(x) has local maxima at x=1+loge2 and local minima at x=e
b. f(x) has local maxima at x=1 and local minima at x=2
c. g(x) has no local minima
d. f(x) has no local maximaSolution in Punjabi
g(x) has local maxima at x=1+loge2 and local minima at x=e
f(x) has local maxima at x=1 and local minima at x=2
g(x) has no local minima
f(x) has no local maxima
The correct Answer is:A, B
Step by step video & image solution for If f(x) = {{:(e ^(x),,"," 0 le x lt 1 ,, ""), (2- e^(x - 1),,"," 1 lt x le 2,, and g(x) = int_(0)^(x) f(t ) dt","),( x- e,,"," 2lt x le 3 ,, ""):} x in [ 1, 3 ] , then a. g(x) has local maxima at x=1+log_(e)2 and local minima at x=eb. f(x) has local maxima at x=1 and local minima at x=2c. g(x) has no local minima d. f(x) has no local maxima by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - MAXIMA AND MINIMA EXERCISE 6
2 Videos
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
49 Videos
- PAIR OF STRAIGHT LINES BOOK - ARIHANT MATHSCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
The figure shows a right triangle with its hypotenuse OB along the y-axis and its vertex A on the parabola y=x2.
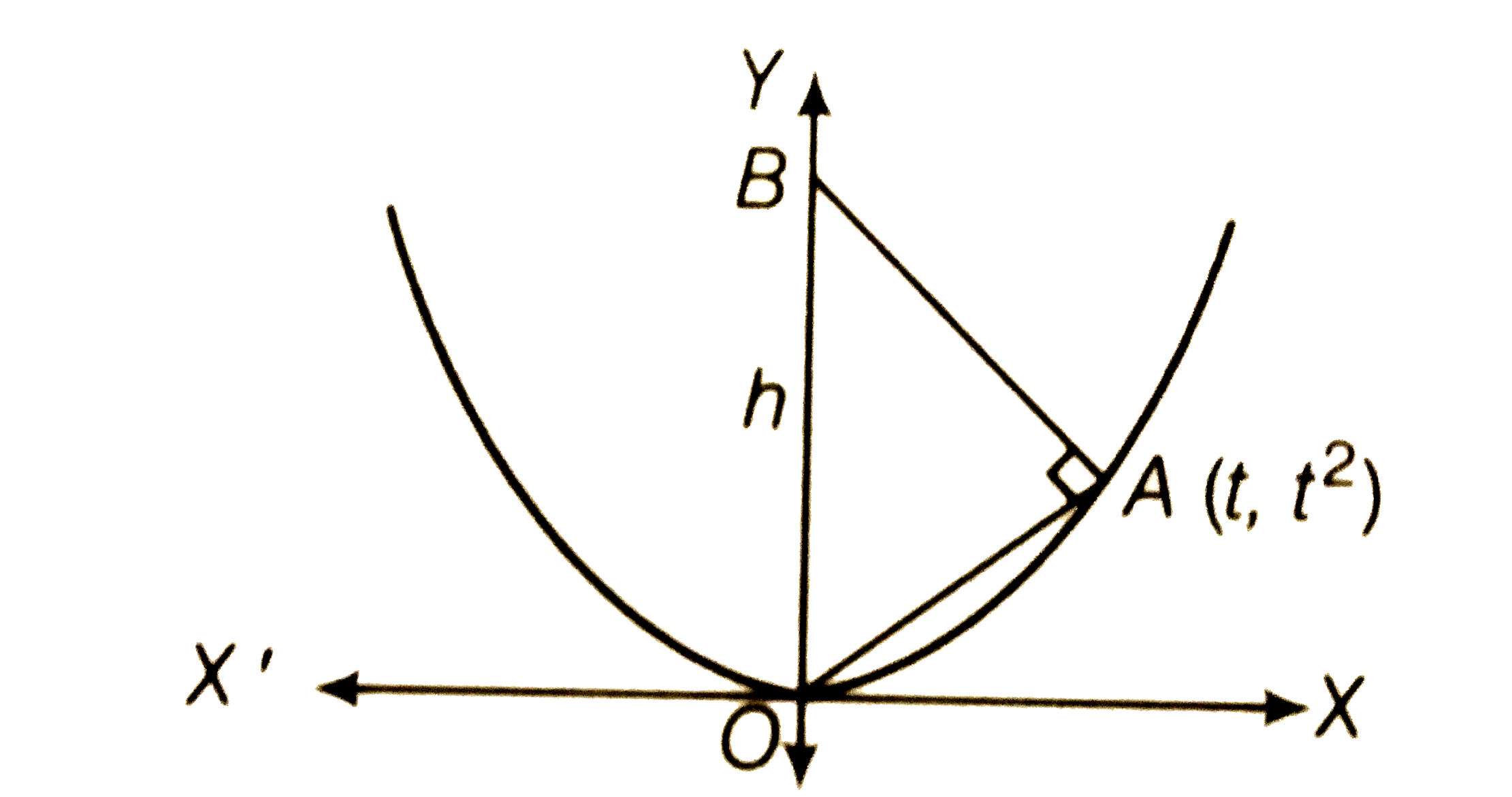
Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of limt→o(h) is equal to
View SolutionLet A=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦andA−1=[16(A2+cA+dI)] Then value of candd are (a) (−6,−11) (b) (6,11) (c) (−6,11) (d) (6,−11)
View SolutionIf the pair of lines ax2+2(a+b)xy+by2=0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
View Solutionf(x) is cubic polynomial with f(x)=18andf(1)=−1 . Also f(x) has local maxima at x=−1andf′(x) has local minima at x=0 , then the distance between (−1,2)and(af(a)), where x=a is the point of local minima is 2√5 f(x) is increasing for x∈[1,2√5) f(x) has local minima at x=1 the value of f(0)=15
View Solutionf(x)={cx,0≤x12−cx−1,1<x≤2andg(x)=∫x0f(t)dt,x∈x−c,2<x≤3 [1,3] then g(x) has local maxima at x=1+ln2 and local minima at c=c local maxima at x=1 and local minima at x=2 no local maxima no local minima
View Solutione total number of local maxima and local minima of the function 'f (x)={(2+x)^(^^)3,-3
View SolutionIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩ex,0≤x<12−ex−1,1<x≤2andg(x)=∫x0f(t)dt,x−e,2<x≤3
x∈[1,3], then
View SolutionFind the local maxima and local minima, and the corresponding local maximum and local minimum values of the following functions:
(i) f(x)=x√1−x, where x>0
(ii) f(x)=x(x−1)(x−4), where 1<x<4
View SolutionThe total number of local maxima and local minima of the function f(x) = {{:( (2 + x)^(3) "," , -3 lt x le -1) , (x^(2//3) "," , -1 lt x lt 2):} is
View SolutionA cubic polynomial function f(x) has a local maxima at x=1 and local minima at x=0 .If f(1)=3 and f(0)=0, then f(2) is
View SolutionThe total number of local maxima and local minima of the function :
f(x)={(2+x)3,−3<x≤−1x23,−1<x<2 is :
View Solutionf(x)=⎧⎪⎨⎪⎩x0≤x≤12−ex−11≤x≤2x−e2≤x≤3 g'(x)=f(x) , x∈[1,3] then
(A) g(x) has no local maxima
(B) g(x) has no local minima
(C) g(x) has local maxima at x=1+ln2 and local minima at x=e
(D) g(x) has local minima at x=1+2ln2 and local maxima at x=e
View SolutionFind the intervals in which f(x)=∫x0{et−1)(t+1)(t−2)(t+4). dt increases and decreases. Also find the points of local maxima and local minima of (x).
View Solutionf(x)=⎧⎪⎨⎪⎩x,0≤x≤12−ex−1,1≤x≤2x−e,2<x≤3 तथा g(x)=π∫0f(t)dt,x∈[0,3] तो g(x) रखता है।
View Solutionthe total number of local maxima and local minima of the function f(x) = {((2+x)^3; -3 (x^3; -1 < x < 2 ) is
View Solutione total number of local maxima and local minima of the function f(x) = {(2+x)^3, -3
View Solution
