If is a function , we say has property I. If for all real numbers x. II. for all real numbers x. How many linear functions, have both property I and Il ?
0
2
3
Infinite
The correct Answer is:B
To solve the problem, we need to find the linear functions f(x) that satisfy the two given properties:
1. f(f(x))=x for all real numbers x.
2. f(−f(x))=−x for all real numbers x.
Step 1: Assume the form of the linear function
Let’s assume that f(x) is a linear function of the form:
f(x)=ax+b
where a and b are constants.
Step 2: Apply the first property
Now, we apply the first property f(f(x))=x:
f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b
Setting this equal to x:
a2x+ab+b=x
This gives us two equations by comparing coefficients:
1. a2=1
2. ab+b=0
Step 3: Solve the first set of equations
From the first equation a2=1, we find:
a=1ora=−1
Now, we will analyze each case for a.
Case 1: a=1
Substituting a=1 into the second equation:
1⋅b+b=0⟹2b=0⟹b=0
Thus, one possible function is:
f(x)=1⋅x+0=x
Case 2: a=−1
Substituting a=−1 into the second equation:
−1⋅b+b=0⟹−b+b=0⟹0=0
This does not provide any restriction on b, so b can be any real number. Thus, another possible function is:
f(x)=−1⋅x+b=−x+b
Step 4: Apply the second property
Now we apply the second property f(−f(x))=−x:
1. For f(x)=x:
f(−f(x))=f(−x)=−x(This holds true)
2. For f(x)=−x+b:
f(−f(x))=f(−(−x+b))=f(x−b)=−(x−b)+b=−x+b+b=−x+2b
Setting this equal to −x:
−x+2b=−x⟹2b=0⟹b=0
Thus, this function simplifies to:
f(x)=−x
Conclusion
The two linear functions that satisfy both properties are:
1. f(x)=x
2. f(x)=−x
Thus, there are 2 linear functions that have both properties.
Final Answer
The number of linear functions that have both properties I and II is 2.
---
2. f(−f(x))=−x for all real numbers x.
f(x)=ax+b
where a and b are constants.
f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b
Setting this equal to x:
a2x+ab+b=x
This gives us two equations by comparing coefficients:
1. a2=1
2. ab+b=0
a=1ora=−1
1⋅b+b=0⟹2b=0⟹b=0
Thus, one possible function is:
f(x)=1⋅x+0=x
−1⋅b+b=0⟹−b+b=0⟹0=0
This does not provide any restriction on b, so b can be any real number. Thus, another possible function is:
f(x)=−1⋅x+b=−x+b
1. For f(x)=x:
f(−f(x))=f(−x)=−x(This holds true)
f(−f(x))=f(−(−x+b))=f(x−b)=−(x−b)+b=−x+b+b=−x+2b
Setting this equal to −x:
−x+2b=−x⟹2b=0⟹b=0
Thus, this function simplifies to:
f(x)=−x
1. f(x)=x
2. f(x)=−x
The number of linear functions that have both properties I and II is 2.
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)
22 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 12
4 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
Knowledge Check
If f(x)=2 for all real numbers x, then f(x+2)=
A0B2C3DxFor all real numbers x , f(2x) = x2−x+3. An expression for f(x) in terms of x is
A2x2−2x+3B4x2−2x+3Cx24−x2+3Dx22−x2+3A function f(x) is defined as even if and only if f(x)=f(−x) for all real values of x. Which one of the following graphs represents an even function f(x) ?
A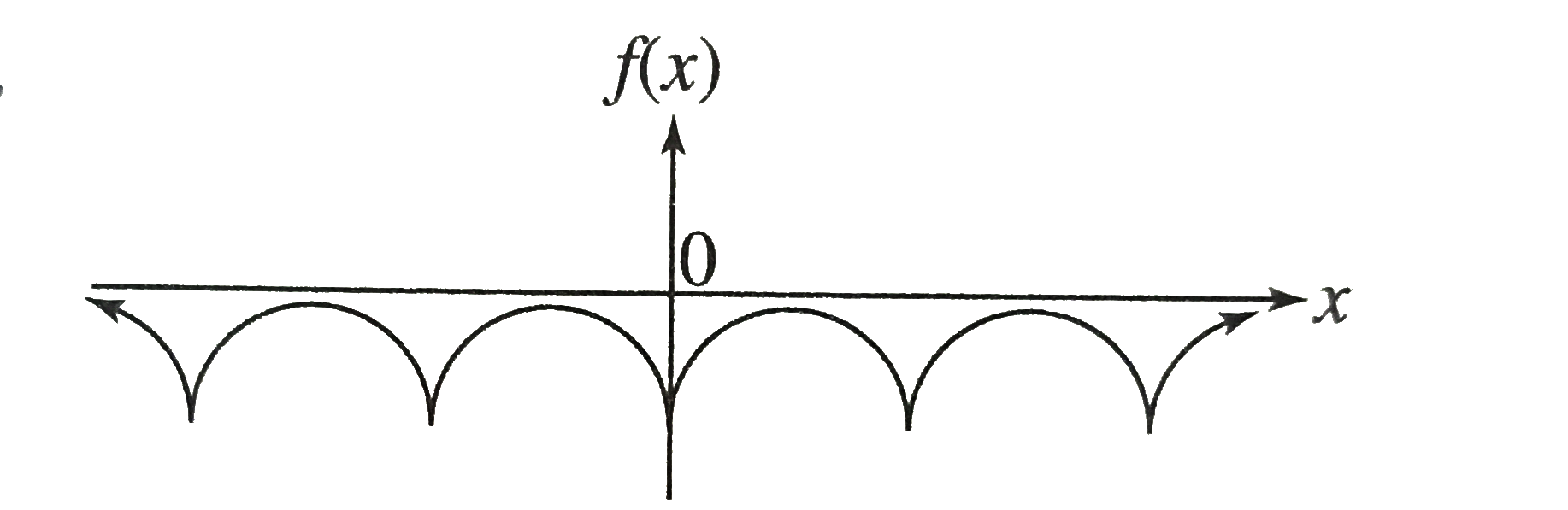 B
B C
C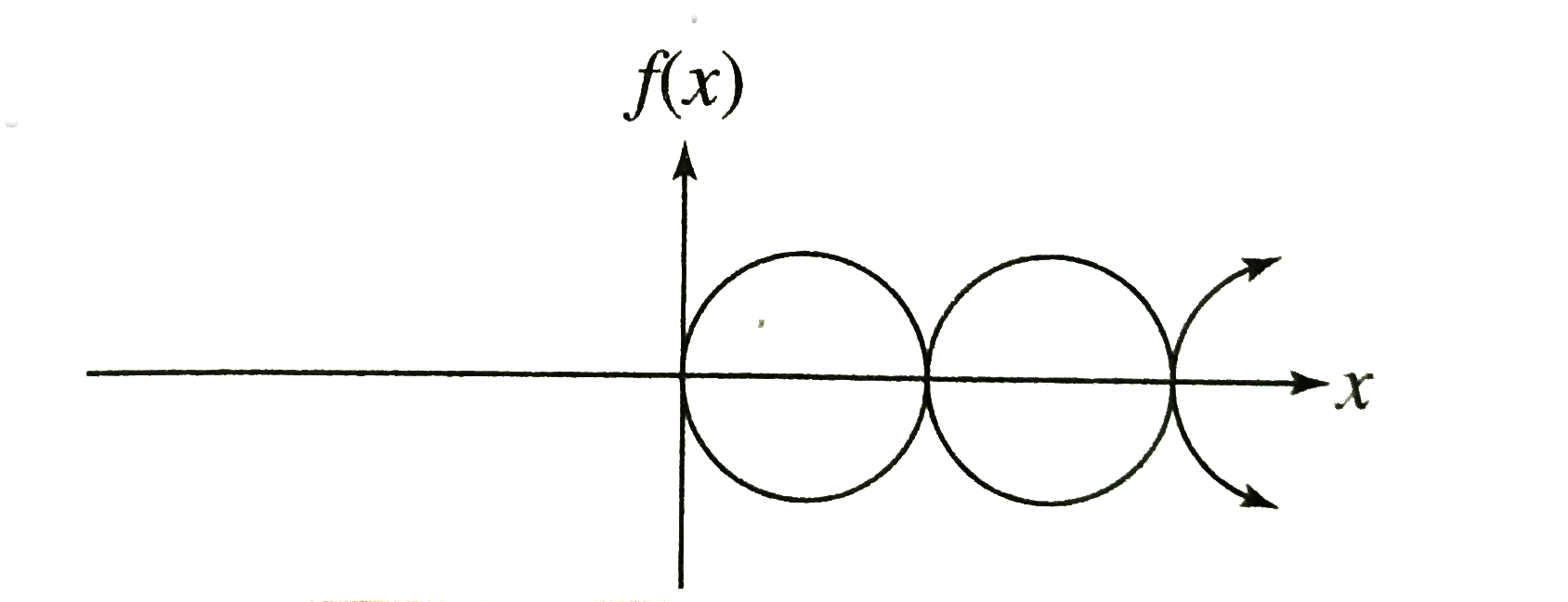 D
D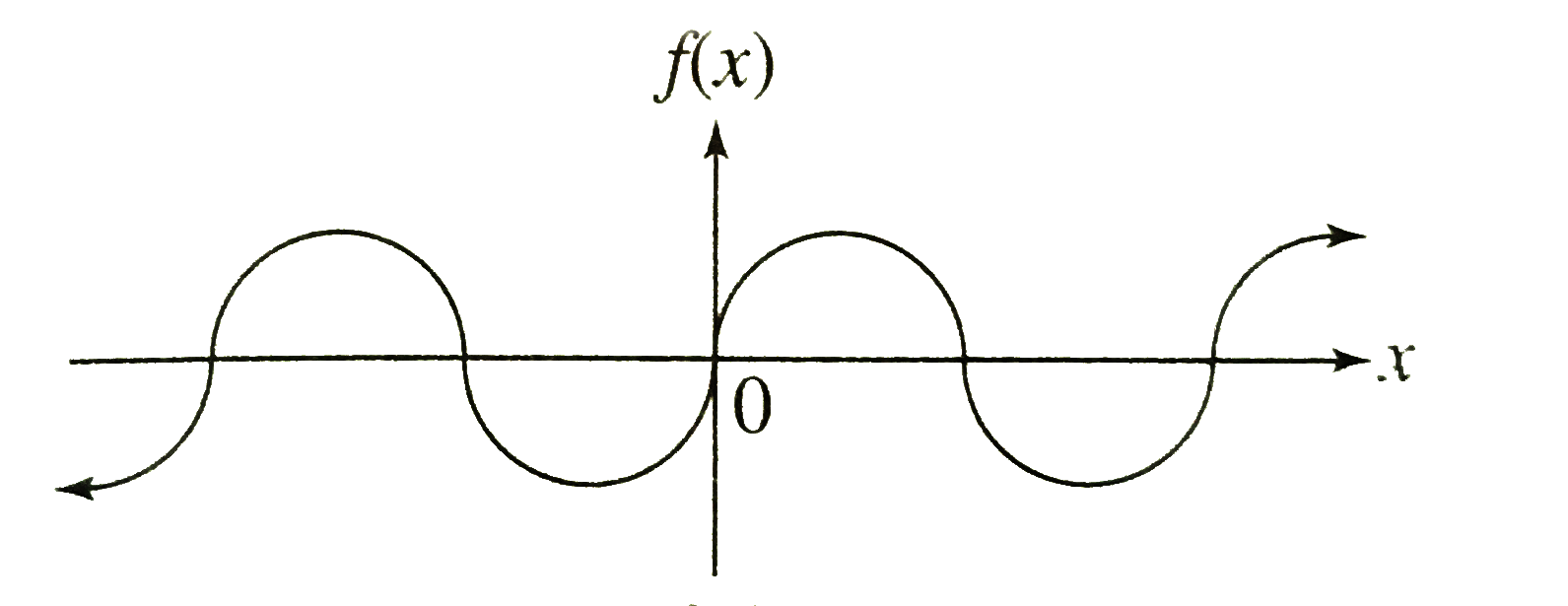
Let f and g real functions defined by f(x)=2x+1 and g(x)=4x−7.
(i) For what real number x,f(x)=g(x)?
(ii) for what real number x,f(x)<g(x)?
View SolutionIf f be a function defined as f(x) = p for each x∈R, where p is a real number, then f is called
View SolutionLet f be a function satisfying of x. Then f(xy)=f(x)y for all positive real numbers xandy. If f(30)=20, then find the value of f(40).
View SolutionA certain function f(x) has the property that f(3x)=αf(x) for all positive real values of x and f(x)=1−|x−2| for 1≤x≤3, limx→2(f(x))cosec(πx2) is
View SolutionProve that the function f : R→R where R is the set of all real numbers, defined as f (x) = 3x+4 is one-one and onto . Also find the inverse function of f.
View Solution
