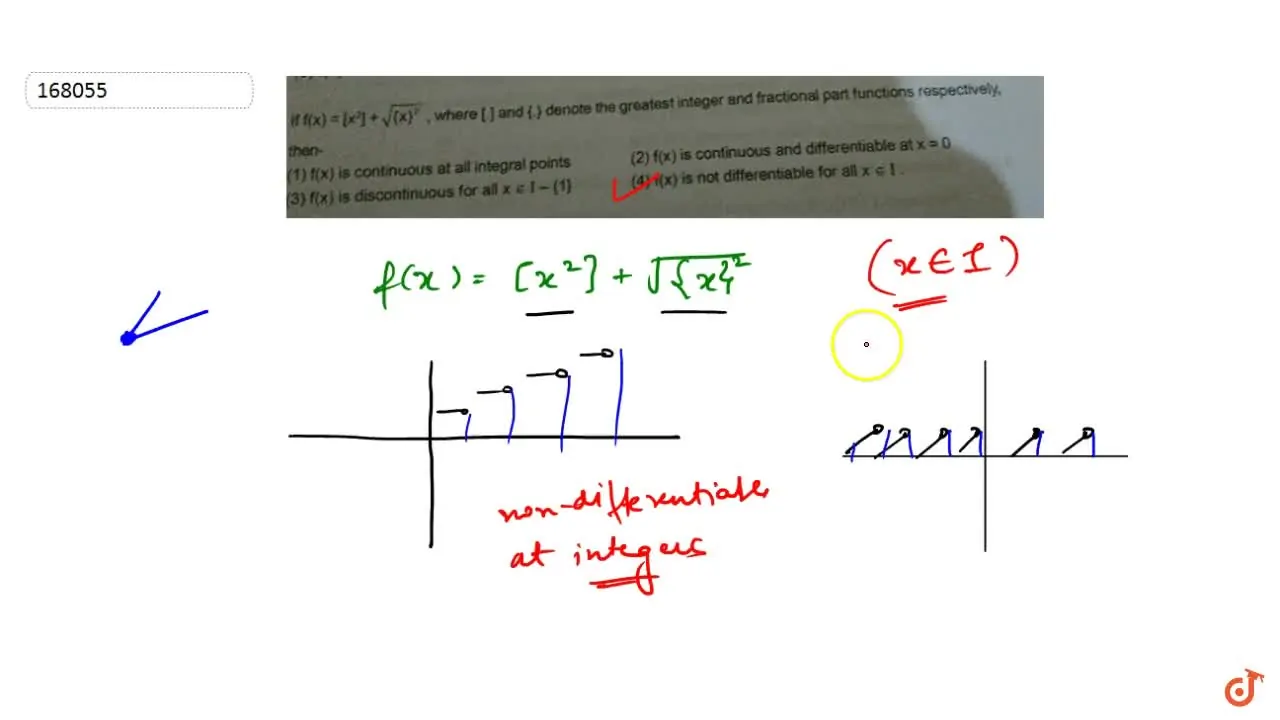
If f(x)=[x2]+√{x}2, where [] and {.} denote the greatest integer and fractional part functions respectively,then
f(x) is continuous at all integer points
f(x) is continuous and differentiable at x=0
f(x) is continuous for all x∈Z−(1)
f(x) is not differerntiable on Z
The correct Answer is:C
Let k be any integer. Then,
f(x)=k2+x−kfor all x∈[k,k+1]
⇒f(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩x+2−1≤x<0x0≤x<2x+22≤x<3x+63≤x<4 and so on.
Clearly, f(x) is continuous and differerntiable at x=1
At all other integer points f(x) discontinuous and hence non-differentiable
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
Similar Questions
Solve : [x]2=x+2{x}, where [.] and {.} denote the greatest integer and the fractional part functions, respectively.
View Solutionf(x)=[x2]−{x}2, where [.] and {.} denote the greatest integer function and the fractional part function , respectively , is
View SolutionIf f(x)=x+{−x}+[x], where [x] and {x} denotes greatest integer function and fractional part function respectively, then find the number of points at which f(x) is both discontinuous and non-differentiable in [−2,2].
View SolutionThe range of function f(x) = logx([x]) , where [.] and {.} denotes greatest integer and fractional part function respectively
View SolutionThe number of non differentiability of point of function f(x)=min([x],{x},∣∣∣x−32∣∣∣) for x∈(0,2), where [.] and {.} denote greatest integer function and fractional part function respectively.
View SolutionIf f(x)=tanxx, then find limx→0([f(x)]+x2)1[f(x)], where [.] and {.} denotes greatest integer and fractional part function respectively.
View SolutionNumber of solutions of the equation 2x]−3{2x}=1 (where [ . ] and {.} denotes greatest integer and fractional part function respectively
View SolutionThe number of integers in the range of the function f(x)=x−[x]1+{x} x(where [.] and {.} denote the integral part and fractional part functions respectively) is
View SolutionLet f(x)=log{x}[x]
g(x)=log{x}−{x}
h(x)log{x}{x}
where [],{} denotes the greatest integer function and fractional part function respectively.
Domine of h(x) is :View SolutionIf f(x)=⎧⎨⎩[x]+√{x},x<11[x]+{x}2,x≥1, then
[where [.] and {.} represent the greatest integer and fractional part functions respectively]View Solution