If I=∫sin2x(3+4cosx)3dx, then I equals
3cosx+8(3+4cosx)2+C
3+8cosx16(3+4cosx)2+C
3+cosx(3+4cosx)2+C
3−8cosx16(3+4cosx)2+C
The correct Answer is:b
We have, I=2∫cosxsinx(3+4cos)3dx
⇒I=−12∫cosx(3+4cosx)3d(3+4cosx)
⇒I=−12∫t−34t3dt where t=3+4cosx
⇒I=18(1t−32t2)+C
⇒I=2t−316t2+C=8cosx+316(3+4cosx)2+C
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INDEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type3videos
INDEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INDEFINITE INTEGRALSEXERCISE - Exercise61videos
INDEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INDEFINITE INTEGRALSEXERCISE - Chapter Test30videos
INDEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INCREASING AND DECREASING FUNCTIONSEXERCISE - Chapter Test18videos
INCREASING AND DECREASING FUNCTIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test30videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
IfI=∫sin2x(3+4cosx)3dx,thenIequals (a)3cosx+8(3+4cosx)2+C (b) 3+8cosx16(3+4cosx)2+C (c)3cosx(3+4cosx)2+C (d) 3−8cosx16(3+4cosx)2+C
View Solution∫sin2xcos2x+3cosx+2dx
View Solution∫(sin2x−4e3x)dx
View SolutionIf I=∫dx(a2−b2x2)3/2, then I equals
View SolutionIf I=∫dxx4√a2+x2, then I equals
View SolutionIf I=∫2−2dx, then I equals
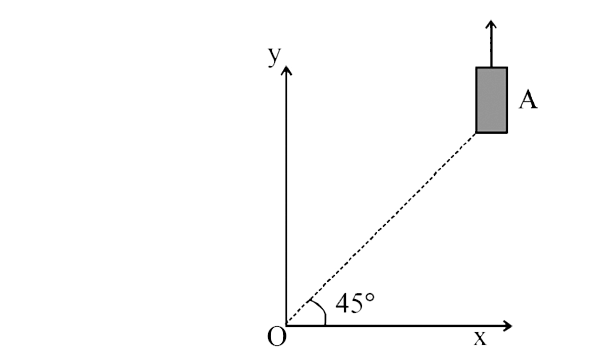
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
 View Solution
View SolutionLet I=∫cos3x1+sin2xdx, then I is equal to (where c is the constant of integration )
View Solution∫sin2(4x+3)dx
View SolutionIf I=∫π−πsin21+axdx,a>0, then I equals
View Solution

