If I(m)=∫π0loge(1−2mcosx+m2)dx, Then match the following lists and choose the correct code. :

Text Solution
The correct Answer is:2
I(m)=∫π0loge(1−2mcosx+m2)dx
⇒I(−m)=∫π0loge(1+2mcosx+m2)dx
=∫π0loge(1+2mcos(π−x)+m2)dx
=∫π0loge(1−2mcosx+m2)dx
=I(m)=I(m)
⇒I(m)+I(−m)=∫π0loge(1−2m2cos2x+m4)dx
put 2x=t
⇒I(m)+(−m)=I(m2)
⇒2I(m)=I(m2)
⇒I(m2)I(m)=2
=I(9)I(3)=2 and I(25)I(5)=2
⇒I(81)I(91)=2 and I(9)I(3)=2
⇒I(81)I(3)=4
|
Topper's Solved these Questions
- DEFINITE INTEGRATION BOOK - CENGAGE ENGLISHCHAPTER - DEFINITE INTEGRATION EXERCISE - NUMERICAL VALUE_TYPE
28 Videos
- DEFINITE INTEGRATION BOOK - CENGAGE ENGLISHCHAPTER - DEFINITE INTEGRATION EXERCISE - JEE MAIN
12 Videos
- DEFINITE INTEGRATION BOOK - CENGAGE ENGLISHCHAPTER - DEFINITE INTEGRATION EXERCISE - LC_TYPE
31 Videos
- CURVE TRACINGBOOK - CENGAGE ENGLISHCHAPTER - CURVE TRACINGEXERCISE - EXERCISES
24 Videos
- DETERMINANTBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer
5 Videos
Similar Questions
Knowledge Check
Match the following lists and then choose the correct code.
 AabcdprsqBabcdrsqpCabcdrqspDabcdpqsr
AabcdprsqBabcdrsqpCabcdrqspDabcdpqsrMatch the following lists and then choose the correct code.
 AabcdqsrpBabcdpsrsCabcdqspsDabcdspqr
AabcdqsrpBabcdpsrsCabcdqspsDabcdspqrMatch the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
If I(m)=∫π0ln(1−2mcosx+m2)dx, then I(1)=
View SolutionLet ∫∞0sinxxdx=α Then match the following lists and choose the correct code. :

View SolutionIf I(m)=∫π0ln(1−2mcosx+m2)dx, then I(1)=
View Solution∫π0log(1+cosx)dx=−π(log2)
View SolutionMatch List I with List II and choose the correct code
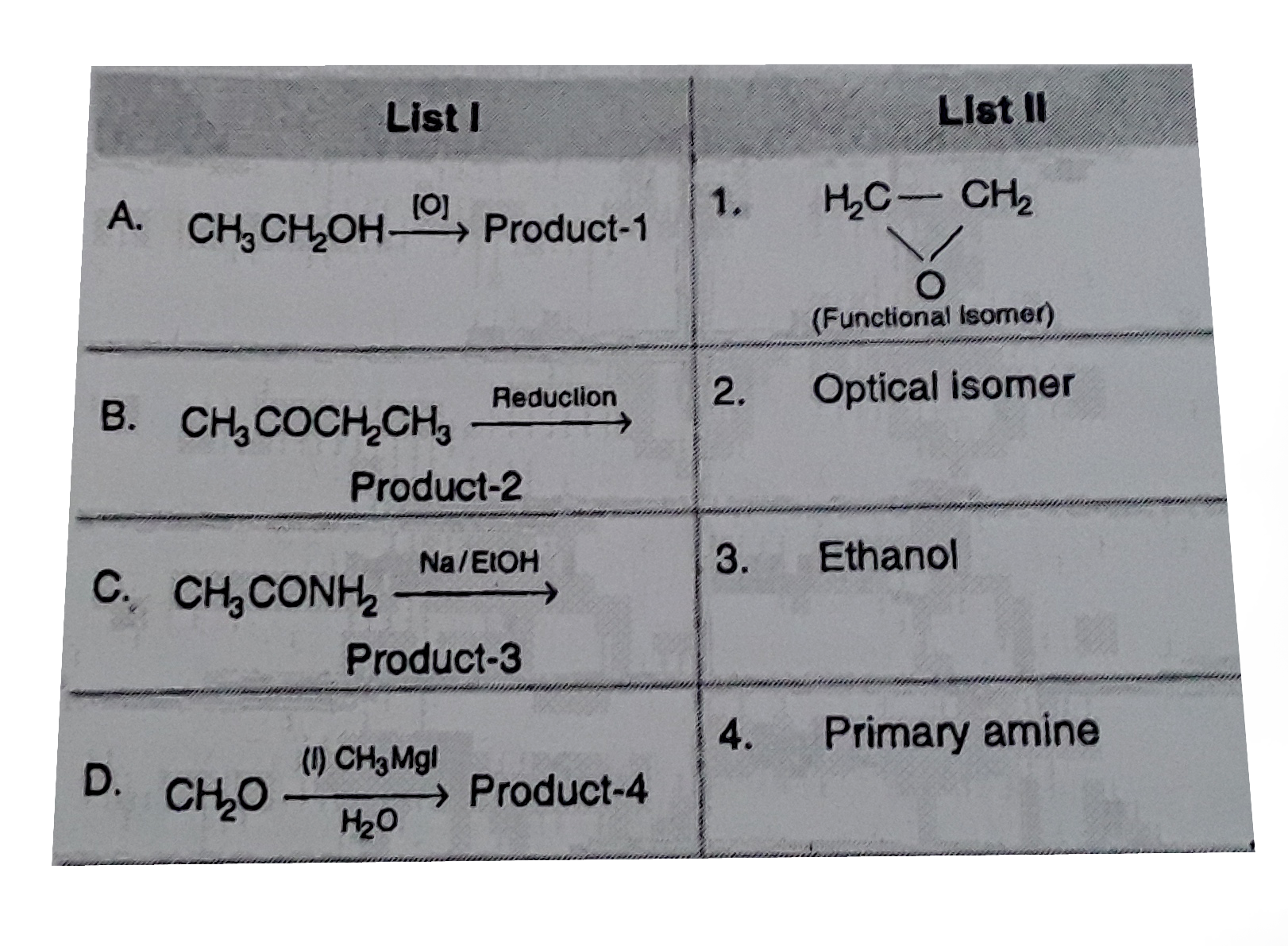
View Solution
