If in a ,CD is the bisector of then CD =
A
B
C
D
Video Solution
Text Solution
Since AD is the bisector of of ABC.
…(i)
Also, in DCB, we have
…(ii)

From (i) and (ii), we have
|
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMACHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
60 Videos
Similar Questions
Knowledge Check
In a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49B49:25C6:1D5:7In the adjoining figure CD is perpendicular on AB. CN is the angle bisector of ∠ACB.∠ACN=50∘,∠NCD is:
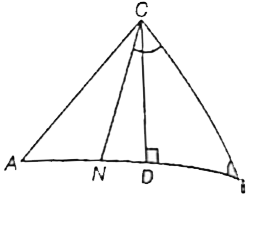 AA)13∠ACBBB)∠CAB−∠CBACC)12(∠CBA−∠BAC)DD)can't be determined
AA)13∠ACBBB)∠CAB−∠CBACC)12(∠CBA−∠BAC)DD)can't be determinedThe ratio of the length and the breadth of a rectangle is 4 : 3 and the area of the rectangle is 1728 sq cm. What is the ratio of the breadth and the area of the rectangle ?
A1 : 38B1 : 24C1 : 42D1 : 48
In the figure , CD is the angle bisector of ∠ECB,∠B=∠ACE. Prove that ∠ADC=∠ACD
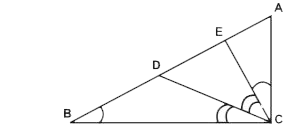
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
View SolutionABC is a equilateral triangle and CD is internal bisector of ∠C. If DC is extended to E in such a way that AC = CE then ∠CAE is-
View SolutionIn ΔABC,AB=5cm,AC=7cm. If AD is the angle bisector of ∠A Then BD:CD is :
View SolutionIn a triangle ABC, internal bisector of ∠ABC and external bisector of ∠ACB meet in D. Which one of the following is true ?
View Solution
