If in a $△ A B C, A = \frac{π}{3} and A D$ is the median, then

A

$2 A D^{2} = b^{2} + c^{2} + b c$

B

$4 A D^{2} = b^{2} + c^{2} + b c$

C

$6 A D^{2} = b^{2} + c^{2} + b c$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

|

Answer

Step by step video, text & image solution for If in a triangleABC, A=pi/3 and AD is the median, then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In an isosceles $△ A B C$ , If $A B = A C$ and AD is the median, then $¯ ¯¯¯¯ ¯ A D \cdot ¯ ¯¯¯¯ ¯ B C =$
A $¯ ¯¯¯¯ ¯ A C$
B $¯ ¯¯¯¯ ¯ B D$
C $1$
D $0$
Question 2 - Select One
If in a $! A B C, ∠ A = π / 3$ and AD is a median , then
A $2 A D^{2} = b^{2} + c^{2} + b c$
B $4 A D^{2} = b^{2} + c^{2} + b c$
C $6 A D^{2} = b^{2} + c^{2} + b c$
Dnone of these
Question 3 - Select One
In $△ A B C$ , if D is the midpoint of BC and E is the midpoint of AD then $a r (△ B E D)$ = ?

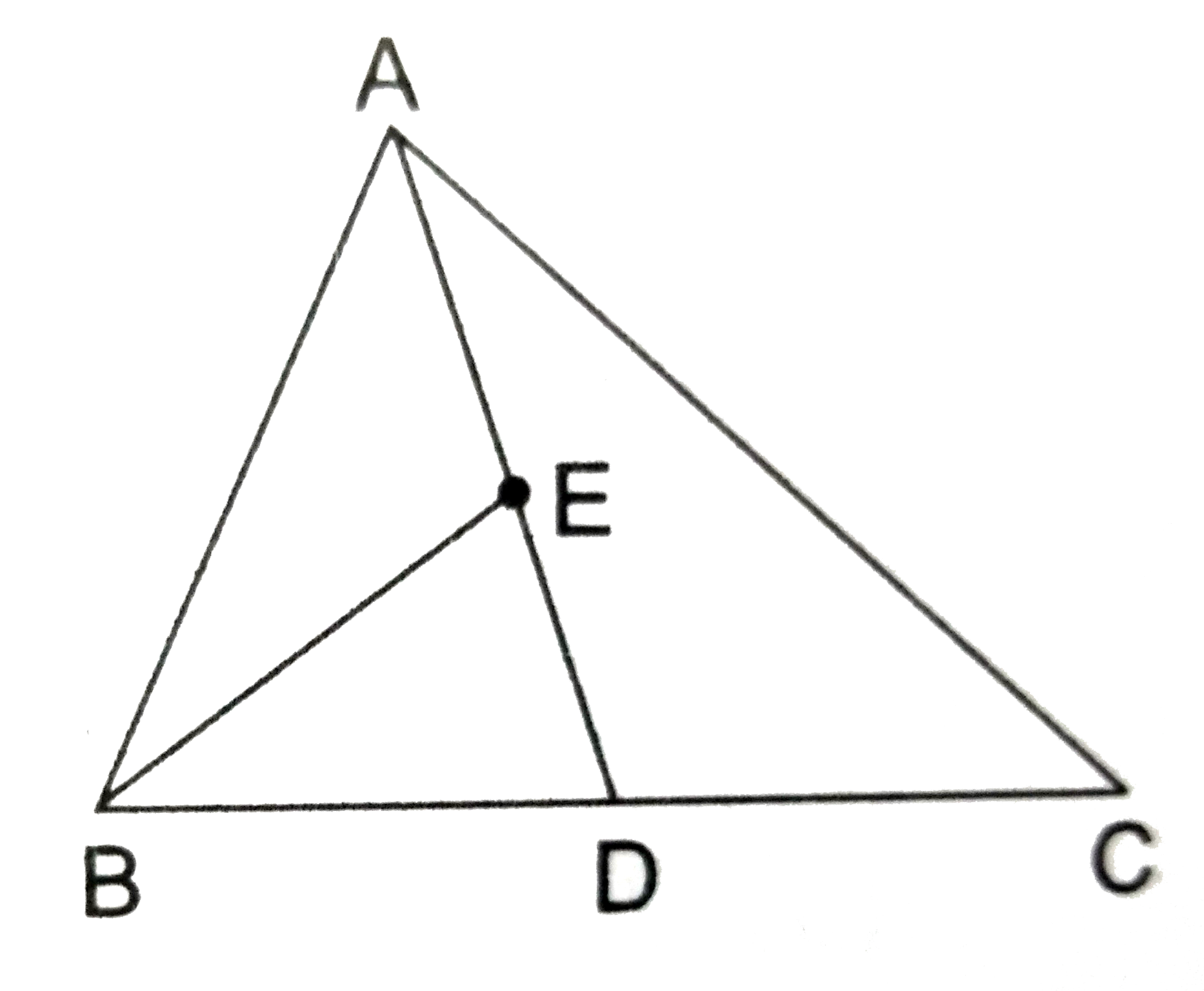A $\frac{1}{2} a r (△ A B C)$
B $\frac{1}{3} a r (△ A B C)$
C $\frac{1}{4} a r (△ A B C)$
D $\frac{2}{3} a r (△ A B C)$

OBJECTIVE RD SHARMA-PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM-Chapter Test

Home
Ask Doubt
Profile