If in ΔABC,b=3cm,c=4cm and the length of the perpendicular from A to the side BC is 2 cm, then how many such triangle are possible ?
The correct Answer is:two

CD=√32−22=√5
BD=√42−22=2√3
Now, area of ΔABC=12.2.(√5+2√3)=12.4.3.sinA
⇒sinA=√5+2√36<1
Also, a>b,a>c
Hence, A can have two values
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.7
Explore 4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.8
Explore 7 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.5
Explore 7 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
The lengths of the sides of a triangle are integral. If the perimeter of the triangle is 6cm, then how many such triangles are possible
View SolutionABC is a triangle right angled at B. If AB=5 cm and BC= 10 cm, then what is the length of the perpendicular drawn from the vertex B to the hypotenuse ?
View Solution
Knowledge Check
Triangles ABC and DEF are similar. If the length of the perpendicular AP from A on the opposite side BC is 2 cm and the length of the perpendicular DQ from D on the opposite side EF is 1 cm, then what is the area of ΔABC?
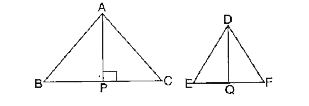 AOne and half times the area of the triangle DEFBFour times the area of triangle DEFCTwice the area of the triangle DEF.DThree times the area of triangle DEF.
AOne and half times the area of the triangle DEFBFour times the area of triangle DEFCTwice the area of the triangle DEF.DThree times the area of triangle DEF.In ΔABC, if : a = 2 cm , b = 3cm and c = 4cm, then ∠A =
Acos−1(124)Bcos−1(1116)Ccos−1(78)Dcos−1(−14)In triangle ABC,BC=8 cm, AC=15 cm and AB=17 cm. The length of the altitude drawn from B on AC is :
A6 cmB7 cmC8 cmD10 cm
In a right-angled triangle ABC ,D is the foot of the perpendicular from B on the hypotenuse AC . If AB=3cm and BC=4cm, what is the area of △ABD?
View SolutionIn triangle ABC,BC=8 cm, AC=15 cm and AB=17 cm. The length of the altitude drawn from B on AC is :
View SolutionIn a triangle ABC, BC = 5 cm, AC = 12 cm and AB = 13 cm. The length of the altitude drawn from B on AC is -----
View SolutionTwo sides of a triangle are 5 cm and 12 cm long. The measure of third sides is an integer in cm. if the tirangles is an obtuse tirangle, then how many such triangles are possible ?
View SolutionIf in a Δ ABC, right angle at A a perpendicular AD is drawn from A on side BC such that AD = 8.4 cm, BD = 4.8 cm then find the length of side BC.
View Solution
