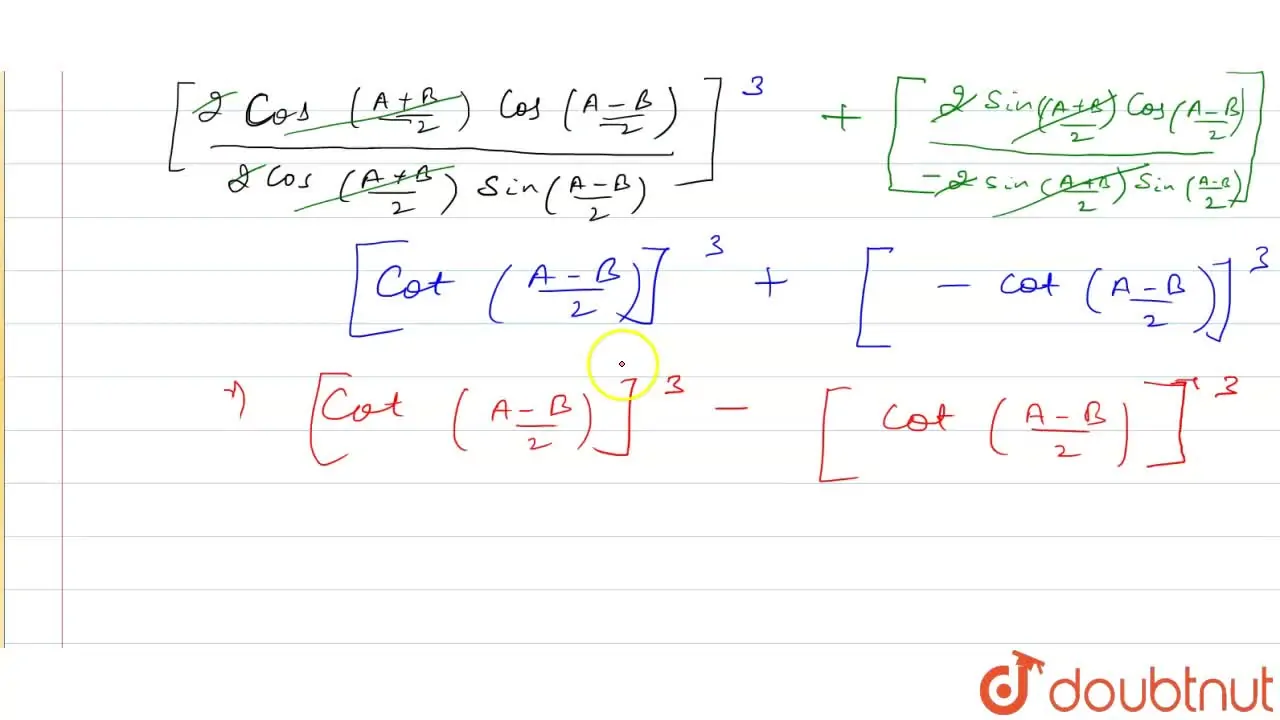
If n is an odd positive interger, then
LHS
, if n is even.
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Solved example15videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Concept App. 3.111videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type6videos
TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS
Similar Questions
Show that 1+sinAcosA+cosB1−sinB=2sinA−2sinBsin(A−B)+cosA−cosB
View SolutionProve that: (cosA+cosB)2+(sinA−sinB)2=4cos2(A+B2) .
View SolutioncosA1−sinA =
View SolutionProve that: (cosA+cosBsinA−sinB)n+(sinA+sinBcosA−cosB)n={2cotn(A−B2),if n is even, 0 if n is odd,
View SolutionProve that: (cosA+cosBsinA−sinB)n+(sinA+sinBcosA−cosB)n={2cotn(A−B2),ifniseven0,ifnisodd,
View SolutionProve that:
(cosA+cosB)2+(sinA+sinB)2=4cos2(A−B)2View SolutionIf cosA+cosB=m and sinA+sinB=n then sin(A+B)=
View Solution(sinA+cosA)2+(sinA−cosA)2=
View SolutionProve that: 1+cosA+sinA1+cosA−sinA=1+sinAcosA
View SolutionProve that:
tan(A+B)2+tan(A−B)2=2sinAcosA+cosBView Solution