If o be the sum of odd terms and E that of even terms in the expansion of (x+a)n prove that: (i)O2−E2=(x2−a2)n (ii) 4OE=(x+a)2n−(x−a)2n (iii) 2(O2+E2)=(x+a)2n+(x−a)2n
The correct Answer is:N/a
(x+a)n=nC0.xn+nC1.xn−1.a
+nC2.xn−2.a2+nC3.xn−3.a3
+....+nCn−1.x.an−1+nCn.an
=[^(n)C0.xn+nC2.xn−2.a2+nC4.xn−4
.a4+....]+[.nC1.xn−1.a
+nC3.xn−3.a3+nC5.xn−5.a5+.....]
⇒ (x+a)n=O+E (Given)....(1)
and (x−a)n=nC0.xn−nC1.xn−1.a+nC2.Xn−2.a2
−nC3.xn−3.a3+....+nCn−1.x.(−a)n−1)
+nCn.(−a)n
=[.nC0xn+nC2xn−2.a2+nC4.xn−4.a4
+......]−[.nC1.xn−1.a
+nC3.xn−3a3+nC5.xn−5.a5+.....]
⇒(x−a)n=O−E ......(2)
(i)L.H.S.=O2−E2
=(O+E).(O−E)
=(x+a)n.(x−a)n
=[(x+a).(x−a)]n
=(x2−a2)n=R.H.S. Hence Proved
(ii) L.H.S. =4OE
=(O−E)2−(O−E)2
=[(x+a)n]2[(x−a)n]2]
=(x+a)2n−(x−a)2n=R.H.S. Hence Proved
(iii)L.H.S.=2(O2+E2)
=(O2+E2+2OE)+(O2+E2−2OE)
=(O+E)2+(O−E)2
[(x+a)n]2+[(x−a)n]2
=(x+a)2n+(x−a)2n
=R.H.S. Hence Proved
Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8A
22 Videos
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8B
38 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - MISCELLANEOUS EXERCISE
20 Videos
Similar Questions
Knowledge Check
If P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, then (x+a)2n+(x−a)2n is
(i) P2−Q2
(ii) P2+Q2
(iii) 2(P2+Q2)
(iv) 4PQAP2−Q2BP2+Q2C2(P2+Q2)D4PQ
If A be the sum of odd terms and B be the sum of even terms in the expansion of (x+a)n, prove that A2−B2=(x2−a2)n
View SolutionIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(ii) 4PQ=(x+a)2n−(x−a)2nand
View SolutionIf the sum of odd terms and the sum of even terms in the expansion of (x+a)n are p and q respectively then p2+q2=
View SolutionIf P and Q are the sum of odd terms and the sum of even terms respectively in the expansion of (x+a)n then prove that
P2−Q2=(x2−a2)n
View Solution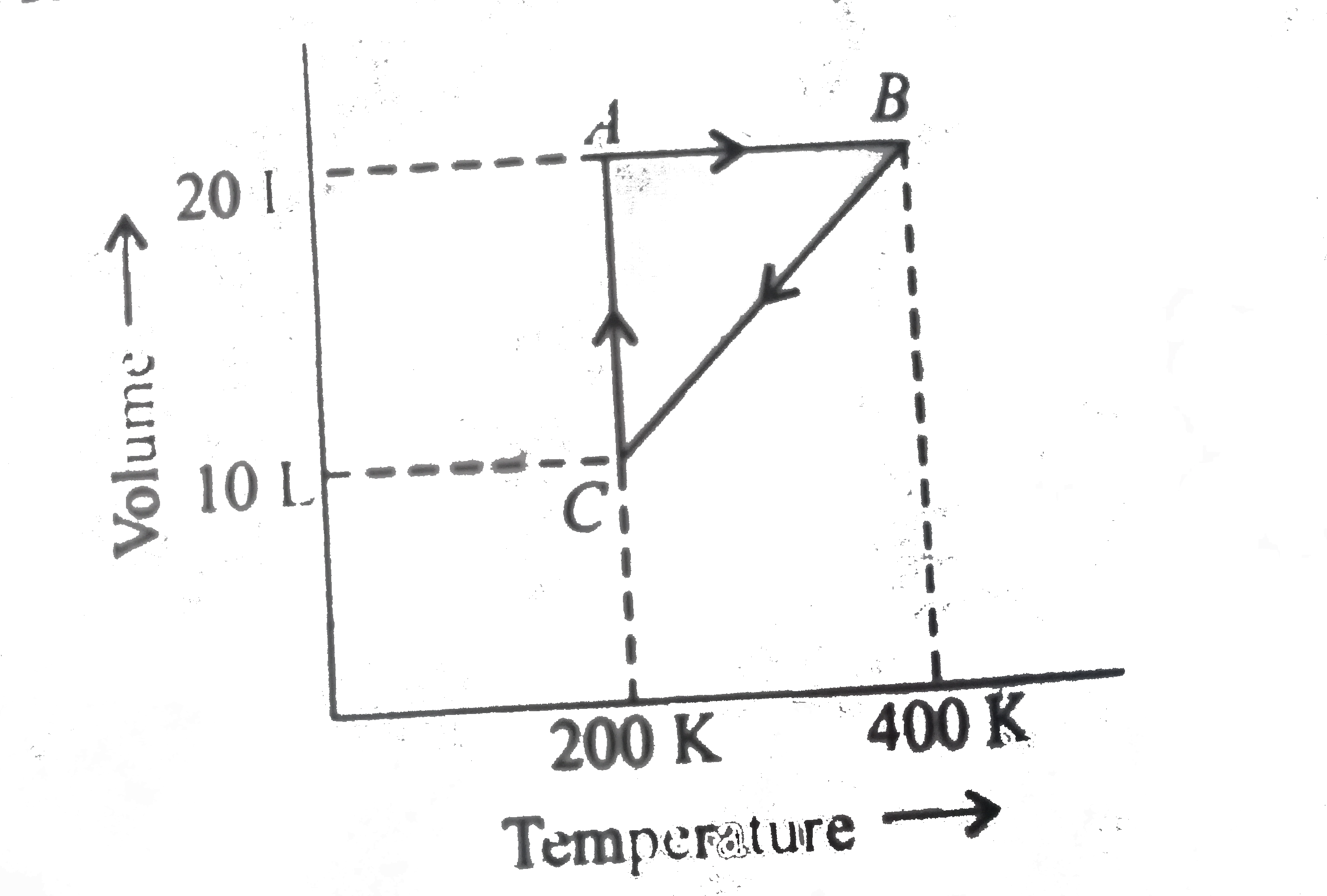
The pressures at A and B in the atmosphere are, respectively,
View SolutionThe sum of the coefficients of middle terms in the expansion of (1+x)2n−1
View SolutionIn the expansion of (x+a)n if the sum of odd terms is P and the sum of even terms is Q, then (a)P2−Q2=(x2−a2)n (b)4PQ=(x+a)2n−(x−a)2n (c)2(P2+Q2)=(x+a)2n+(x−a)2n (d)none of these
View Solution
