If P = (0,1,2) and Q = (4,-2,1), O = (0,0,0) then PˆOQ=Solution in Kannada
π6
π4
π3
π2
The correct Answer is:D
Step by step video, text & image solution for If P = (0,1,2) and Q = (4,-2,1), O = (0,0,0) then P hat O Q = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The mean deviation of the data 2, 9, 9, 3, 6, 9, 4 from the mean is :
02:59View SolutionThe three points whose position vectors are i+2j+3k, 3i+4j+7k, 3i-2j-5k
02:23View SolutionIf P(0,1,2), Q(4,−2,1)and O(0,0,0) are three points then ∠POQ= a. π6 b. π4 c. π3 d. π2
03:36View SolutionIf P(0,1,2),Q(4,−2,1) and O(0,0,0) are three points, then ∠POQ=
View SolutionIf the co-ordinates of the points P and Q are (1,−2,1)and(2,3,4) and O is the origin, then
04:47View SolutionIf P=(0,1,2),Q=(4,−2,1),O=(0,0,0) then ∠POQ is equal to
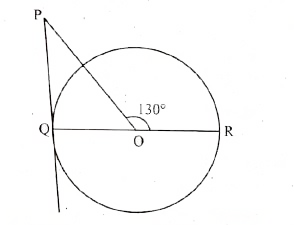
03:29View SolutionO is the centre of the circle QOR is diameter. PQ is tangent to the circle. Given PˆOR=130∘. Find OˆPQ .
 04:12View Solution
04:12View SolutionIf →P=→Q then which of the following is NOT correct? (A)ˆP=ˆQ (B) ∣∣ˆP∣∣=∣∣ˆQ∣∣ (c)ˆPˆQ=ˆQˆP (D) →P+→Q=ˆP+ˆQ
01:48View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
03:30View SolutionIf →PO+→OQ=→QO+→OR, show that the point, P,Q,R are collinear.
02:34View SolutionIn △OPQ right angled at P, OP=7cm , OQ−PQ=1cm . Determine the values of sinQ and cosQ .
03:02View SolutionIn Fig. 10.67, OQ:PQ=3:4 and perimeter of POQ=60cm . Determine PQ, QR and OP . (FIGURE)
02:26View SolutionPQ is a tangent to a circle with centre O at the point P . If △OPQ is an isosceles triangle, then ∠OQP is equal to :
06:07View SolutionIf P(0,1,2), Q(4,−2,1)and O(0,0,0) are three points then ∠POQ= a. π6 b. π4 c. π3 d. π2
03:24View SolutionLet O(0,0),P(3,4),Q(6,0) be the vertices of the triangle OPQ. The point R inside the triangle OPQ is such that the triangle OPR,PQR and OQR are of equal area. The coordinates of R are
04:51View Solution

