If P (-6,-3) and Q (-1, 9), then complete the following
acitvity to find PQ .
Let P(x1,y1) and Q(x2,y2)
x1=−6,y1=−3,x2=−1 and y2=9
PQ=√□ [Distance formula]
∴PQ=√□+□
∴PQ=√□
∴PQ=□
Actively :
√(x2−x1)2+(y2−y1)2 ...[Distance formula]
∴PQ=√25+144
∴PQ=√169
∴PQ=13
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - 6.4 1mark each9videos
COORDINATE GEOMETRY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - 6.5 1mark each3videos
COORDINATE GEOMETRY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - 6.2 1mark each5videos
COORDINATE GEOMETRY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions10videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - FINANCIAL PLANNING EXERCISE - ASSIGNEMENT 4.44videos
FINANCIAL PLANNING
Similar Questions
In the given figure,ray PQ touches the circle at point Q. PQ=12, PR=8, complete the following activity to find PS and RS.
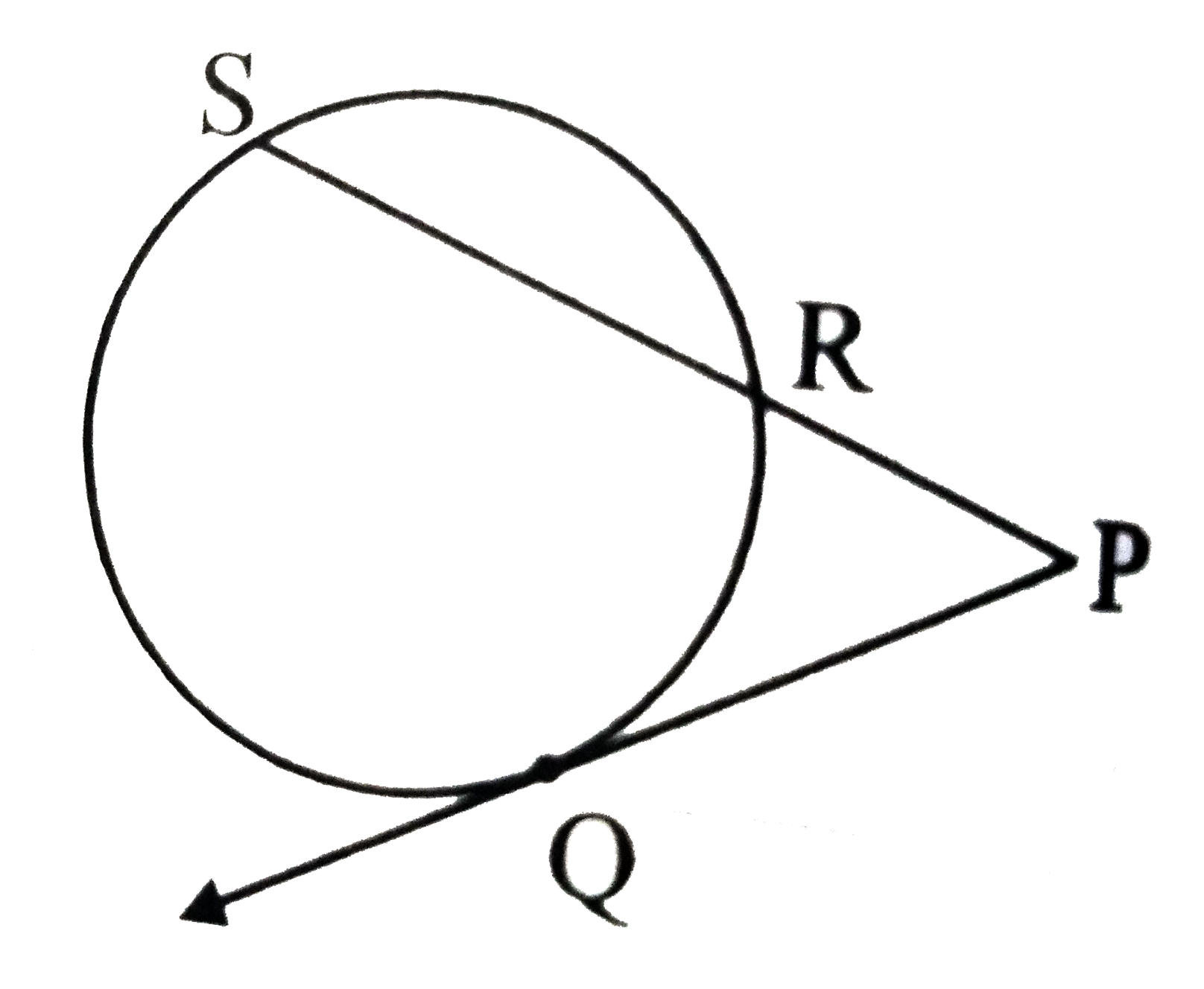 View Solution
View Solution(A) Complete any one out of two activities :
Complete the following activity to show the points P(3,0)Q(6,−2)andR(−3,4) are collinear .
Let P(3,0)=(x1,y1)
Q(6,−2)=(x2,y2)
R(−3,4)=(x3,y3)
slope of a line PQ=y2−□x2−x1=−2−06−3=□ ...(1)
slope of line QR=y3−y2x3−x2=□−(−2)−3−6=4+2−9
=6−9
=□ ... (2)
∴ from (1) and (2)
the slopes of lines PQ and QR are □ and point □ is the
∴ points P,Q and R are collinear .View Solution
Knowledge Check
- Question 1 - Select One
If P(3,2,−4),Q(5,4,−6) and R(9,8,−10) are collinear, then R divides PQ in the ratio
A3:2 internallyB3:2 externallyC2:1 internallyD2:1 externally - Question 2 - Select One
If P(3,2,−4),Q(5,4,−6)andR(9,8,−10) are collinear, then R divides PQ in the ratio
A3:2 internallyB3:1 externallyC2:1 internallyD2:1 externally
If P=(1,2,3,4,5,6,7) and Q=(2,5,8,9), then find P∪Q.
View SolutionP(-3, 7) and Q(1, 9) are two points. Find the point R on PQ such that PR:QR=1:1.
View SolutionIf q=5 and p=−3, then find the value of the following expressions.
8q+9p–17View SolutionIf P=(1,2,3,4,5,6,7) and Q=(2,5,8,9), then find P-Q.
View SolutionIf P=(1,2,3,4,5,6,7) and Q=(2,5,8,9) then find P∩Q.
View SolutionThe coordinates of the points P and Q are respectively (4,-3) and (-1,7). Find the abscissa of a point R on the line segment PQ such that PRPQ=35 .
View Solution

