If P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(i) p2−Q2=(x2−a2)n
To prove that P2−Q2=(x2−a2)n, where P is the sum of the odd terms and Q is the sum of the even terms in the expansion of (x+a)n, we will follow these steps:
Step 1: Write the expansions of (x+a)n and (x−a)n
The binomial expansion of (x+a)n is given by:
(x+a)n=n∑k=0(nk)an−kxk
The expansion of (x−a)n is:
(x−a)n=n∑k=0(nk)(−a)n−kxk=n∑k=0(nk)an−k(−1)n−kxk
Step 2: Add the two expansions
Adding these two expansions, we get:
(x+a)n+(x−a)n=n∑k=0(nk)an−kxk+n∑k=0(nk)an−k(−1)n−kxk
Step 3: Simplify the sum
In this sum, the terms where k is even will add up, and the terms where k is odd will cancel out. Therefore, we can express this as:
(x+a)n+(x−a)n=2⌊n/2⌋∑j=0(n2j)an−2jx2j
This sum represents 2Q (the sum of the even terms).
Step 4: Subtract the two expansions
Now, subtracting the two expansions gives:
(x+a)n−(x−a)n=n∑k=0(nk)an−kxk−n∑k=0(nk)an−k(−1)n−kxk
Here, the terms where k is odd will add up, while the terms where k is even will cancel out. Thus, we can express this as:
(x+a)n−(x−a)n=2⌊(n−1)/2⌋∑j=0(n2j+1)an−(2j+1)x2j+1
This sum represents 2P (the sum of the odd terms).
Step 5: Express P and Q
From the above results, we have:
P=(x+a)n−(x−a)n2
Q=(x+a)n+(x−a)n2
Step 6: Calculate P2−Q2
Using the identity a2−b2=(a+b)(a−b):
P2−Q2=(P+Q)(P−Q)
Substituting the expressions for P and Q:
P+Q=(x+a)nandP−Q=(x−a)n
Thus,
P2−Q2=(x+a)n(x−a)n
Step 7: Simplify the expression
Using the difference of squares:
(x+a)(x−a)=x2−a2
So,
P2−Q2=(x2−a2)n
Conclusion
We have shown that:
P2−Q2=(x2−a2)n
(x+a)n=n∑k=0(nk)an−kxk
(x−a)n=n∑k=0(nk)(−a)n−kxk=n∑k=0(nk)an−k(−1)n−kxk
(x+a)n+(x−a)n=n∑k=0(nk)an−kxk+n∑k=0(nk)an−k(−1)n−kxk
(x+a)n+(x−a)n=2⌊n/2⌋∑j=0(n2j)an−2jx2j
(x+a)n−(x−a)n=n∑k=0(nk)an−kxk−n∑k=0(nk)an−k(−1)n−kxk
(x+a)n−(x−a)n=2⌊(n−1)/2⌋∑j=0(n2j+1)an−(2j+1)x2j+1
P=(x+a)n−(x−a)n2
Q=(x+a)n+(x−a)n2
P2−Q2=(P+Q)(P−Q)
P+Q=(x+a)nandP−Q=(x−a)n
P2−Q2=(x+a)n(x−a)n
(x+a)(x−a)=x2−a2
So,
P2−Q2=(x2−a2)n
P2−Q2=(x2−a2)n
Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - ICSECHAPTER - BINOMIAL THEOREMEXERCISE - CHAPTER TEST
14 Videos
- BINOMIAL THEOREMBOOK - ICSECHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 13 (a)
27 Videos
- BASIC CONCEPTS OF POINTS AND THEIR COORDINATESBOOK - ICSECHAPTER - BASIC CONCEPTS OF POINTS AND THEIR COORDINATESEXERCISE - CHAPTER TEST
2 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - CHAPTER TEST
11 Videos
Similar Questions
Knowledge Check
If P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, then (x+a)2n+(x−a)2n is
(i) P2−Q2
(ii) P2+Q2
(iii) 2(P2+Q2)
(iv) 4PQAP2−Q2BP2+Q2C2(P2+Q2)D4PQ
If P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, prove that
(ii) 4PQ=(x+a)2n−(x−a)2nand
View SolutionIf o be the sum of odd terms and E that of even terms in the expansion of (x+a)n prove that: (i)O2−E2=(x2−a2)n (ii) 4OE=(x+a)2n−(x−a)2n (iii) 2(O2+E2)=(x+a)2n+(x−a)2n
View SolutionIf the sum of odd terms and the sum of even terms in the expansion of (x+a)n are p and q respectively then p2+q2=
View SolutionIf P and Q are the sum of odd terms and the sum of even terms respectively in the expansion of (x+a)n then prove that
P2−Q2=(x2−a2)n
View Solution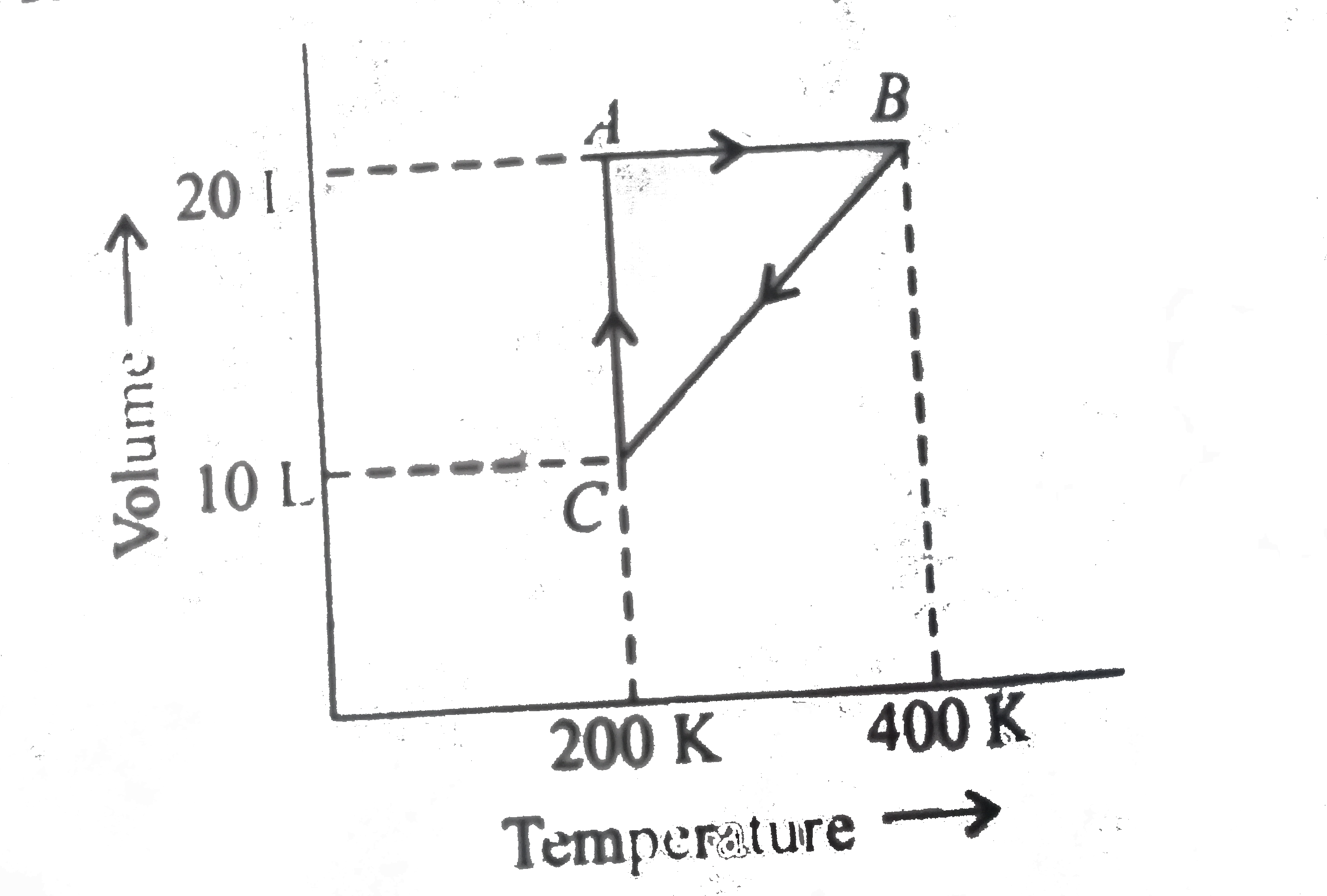
The pressures at A and B in the atmosphere are, respectively,
View SolutionIf the sum of odd terms and the sum of even terms in (x+a)n are p and q respectively then p2+q2=
View SolutionIf A and B respectively denote the sum of the odd terms and sum of the even terms in the expansion of (x+y)n, then the value of (x2−y2)n, is equal to
View Solution
