If P(2,2),Q(−2,4)andR(3,4) are the vertices of ΔPQR then the equation of the median through vertex R is
x+3y+9=0
x−3y+9=0
x−3y−9=0
x+3y−9=0
The correct Answer is:B
Mid-point of point P(2,2) and Q(-2,4) is
(2−22,2+42)
i.e., (0,3)
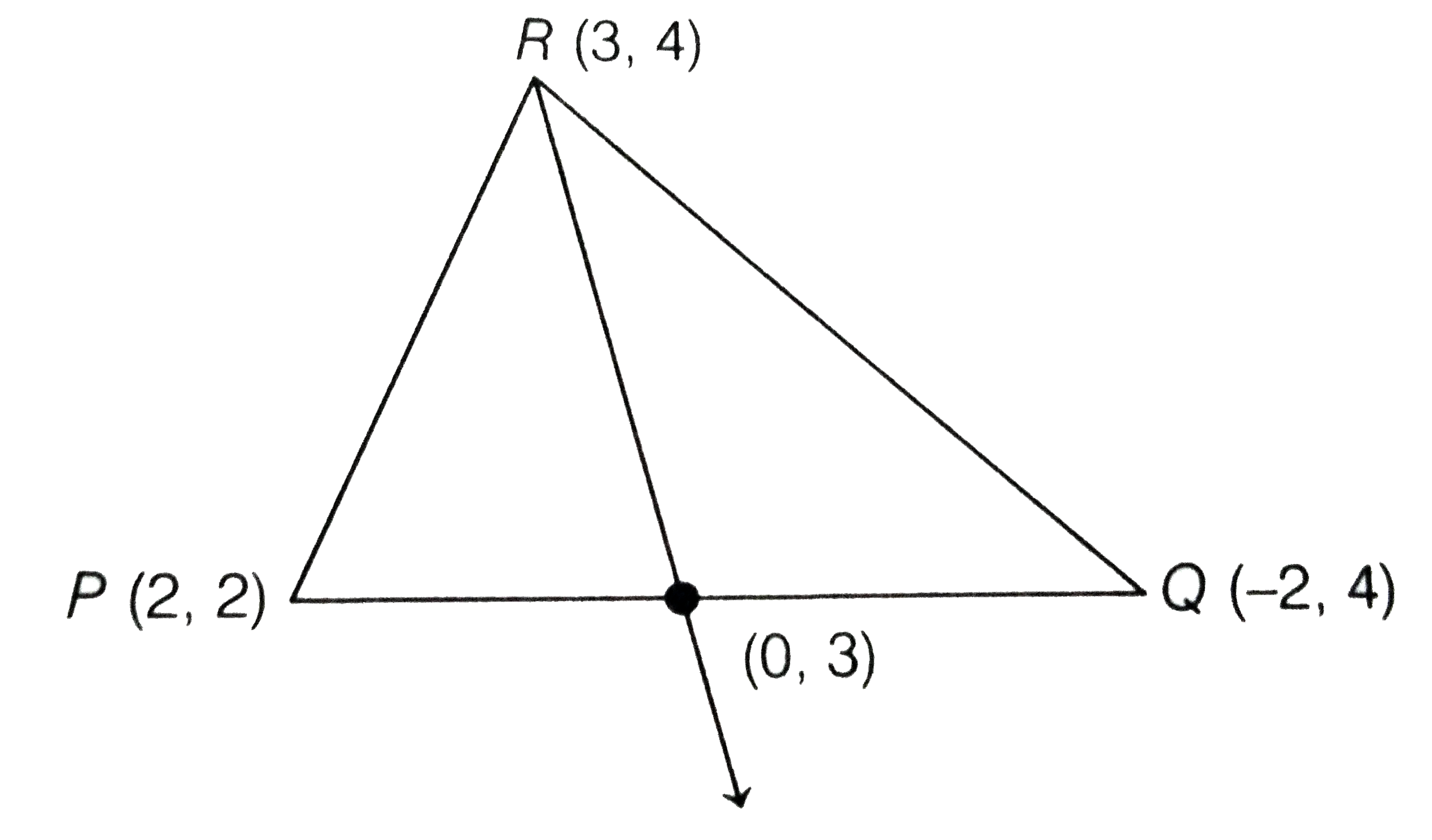
Required equation o median passing through vertex R is
y−4=3−40−3(x−3)
⇒y−4=13(x−3)
⇒3y−12=x−3
x−3y+9=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
If P( 2, 2), Q( -2, 4) and R( 3, 4) are the vertices of ΔPQR then the equation of the median through vertex R is ...
Ax + 3y + 9 = 0Bx - 3y + 9 = 0CX - 3 y - 9 = 0DX + 3 y - 9 = 0P(2,1) , Q (4,-1) , R (3,2) are the vertices of a triangle and if through P and R lines parallel to opposite sides are drawn to intersect in S , then the area of PQRS , is
A6B4C8D12
Consider a triangle with vertices A(1,2),B(3,1), and C(−3,0). Find the equation of altitude through vertex A. the equation of median through vertex A. the equation of internal angle bisector of ∠A.
View SolutionThe vertices of a triangle are (2,0) (0,2) (4,6) then the equation of the median through the vertex (2,0) is
View SolutionIf P(4,7),Q(7,2)R(a,b) and S(3,8) are the vertices of a parallelogram then find the value of a and b.
View SolutionThe vertices of ΔPQR are P(2,1), Q(−2,3), R(4,5). Find equation of the median through the vertex R.
View SolutionConsider a triangle with vertices A(1;2) ;B(3;1) and C(-3;0) Find (i) equation of altitude through vertex A (ii) the equation of median through vertex A (iii) the equation of internal angle bisector of ∠A
View SolutionThe vertices of Δ PQR are P(2,1), Q(−2,3)and R(4,5). Find equation of the median through the vertex R.
View Solution
