Question

If $pandq$
are chosen randomly from the set $\{1,2,3,4,5,6,7,8,9,10\}$
with replacement, determine the probability that the roots of the
equation $x^2+px+q=0$
are real.

Explanation

The roots of `x^(2) + px + q = 0` will be real if `p^(2) - 4q ge 0` or `p^(2) ge 4q`.
The possible values of p and q are given in the following table:

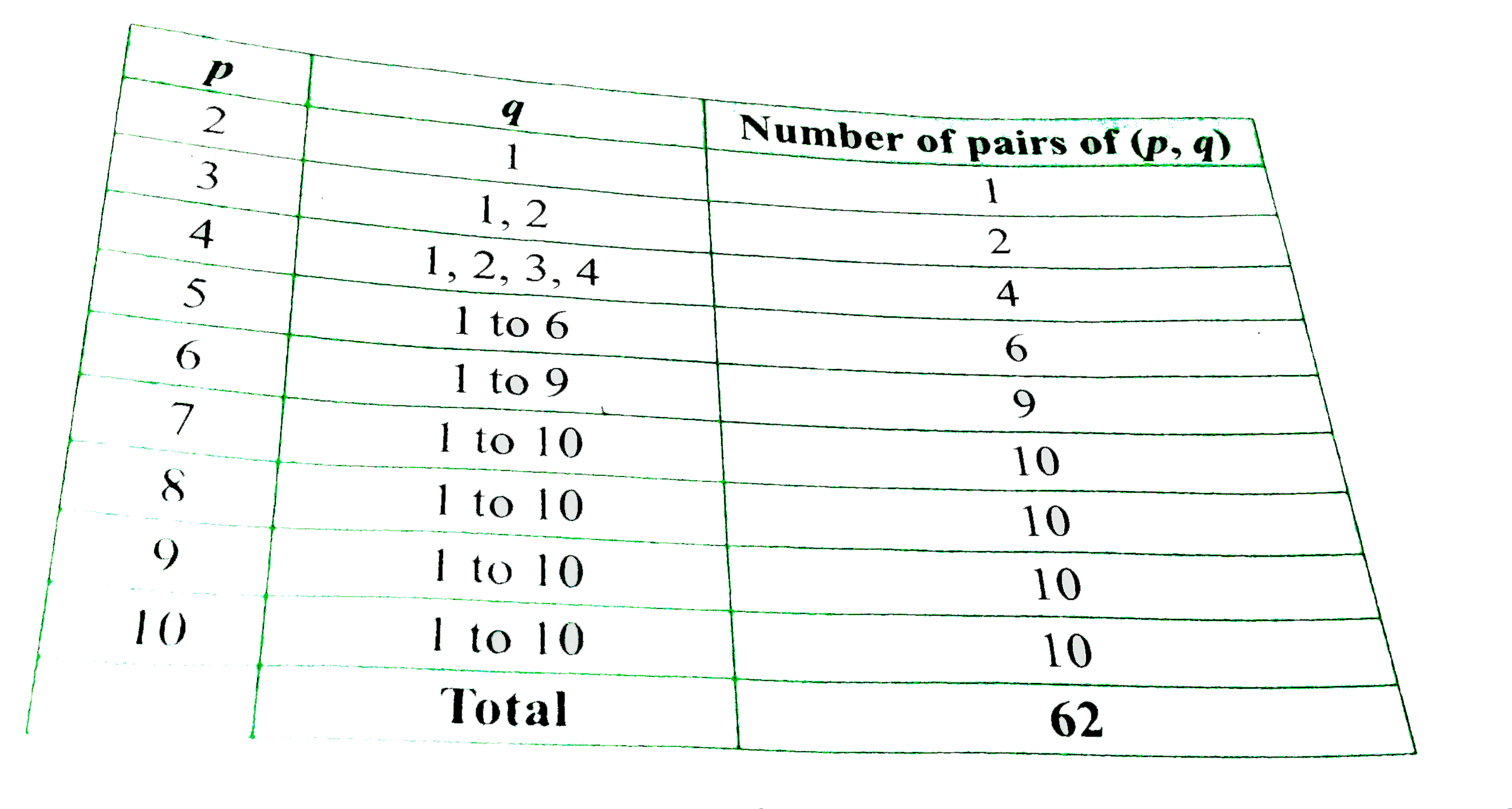
Also, the total number of possible pairs (p,q) = 10 `xx` 10 = 100
`therefore` Required probability = `(62)/(100) = 0.62`