If R={(x,y),x,y,∈W,x2+y2≤4 then domain of R is
{0,1,2,3}
{0,1,2}
{0,1}
{0,2,3}
The correct Answer is:B
To find the domain of the relation R={(x,y)|x,y∈W,x2+y2≤4}, where W is the set of whole numbers, we will follow these steps:
Step 1: Understand the condition
The condition x2+y2≤4 represents a circle with a radius of 2 centered at the origin in the Cartesian plane. Since x and y must be whole numbers, we need to find all pairs (x,y) that satisfy this condition.
Hint: Remember that whole numbers are non-negative integers (0, 1, 2, ...).
Step 2: Set values for x
We will consider different values for x starting from 0 and moving upwards, as x must be a whole number.
1. For x=0:
02+y2≤4⟹y2≤4⟹y=0,1,2
Possible pairs: (0,0),(0,1),(0,2)
2. For x=1:
12+y2≤4⟹1+y2≤4⟹y2≤3⟹y=0,1
Possible pairs: (1,0),(1,1)
3. For x=2:
22+y2≤4⟹4+y2≤4⟹y2≤0⟹y=0
Possible pair: (2,0)
Step 3: Collect all unique x values
From the pairs we found, the possible values of x are:
- From x=0: 0
- From x=1: 1
- From x=2: 2
Step 4: Compile the domain
The domain of the relation R consists of all unique x values we found:
Domain of R={0,1,2}
Final Answer:
The domain of R is {0,1,2}.
---
The condition x2+y2≤4 represents a circle with a radius of 2 centered at the origin in the Cartesian plane. Since x and y must be whole numbers, we need to find all pairs (x,y) that satisfy this condition.
We will consider different values for x starting from 0 and moving upwards, as x must be a whole number.
02+y2≤4⟹y2≤4⟹y=0,1,2
Possible pairs: (0,0),(0,1),(0,2)
12+y2≤4⟹1+y2≤4⟹y2≤3⟹y=0,1
Possible pairs: (1,0),(1,1)
22+y2≤4⟹4+y2≤4⟹y2≤0⟹y=0
Possible pair: (2,0)
From the pairs we found, the possible values of x are:
- From x=0: 0
- From x=1: 1
- From x=2: 2
The domain of the relation R consists of all unique x values we found:
Domain of R={0,1,2}
The domain of R is {0,1,2}.
Topper's Solved these Questions
- RELATION AND FUNCTIONSBook:ICSEChapter:RELATION AND FUNCTIONSExercise:MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
Explore 32 Videos
- QUADRATIC EQUATIONSBook:ICSEChapter:QUADRATIC EQUATIONSExercise:CHAPTER TEST
Explore 24 Videos
- RELATIONS AND FUNCTIONSBook:ICSEChapter:RELATIONS AND FUNCTIONSExercise:EXERCISE 2 (g)
Explore 37 Videos
Similar Questions
Knowledge Check
Given R={(x,y):x,y∈W,x2+y2=169}, then the domain of R is
A{0,5, 12, 13}B{-13,-12,-5, 0,5, 12, 13}C{0, 1, 2, 3, ... 13}D{0,±1,±2,...±13}If R={(x,y):x,y∈W,2x+y=8}, then domain of R is
A{0, 1, 2, 3, 4, 5}B{0,1,2,3,4,5,6}C{0,1,2,3,4}D{0, 1, 2, 3}Let A = {1,2,3,4,5,6} and R be the relation defined on A by R={(x,y):x,y∈A,x divides y}, then range of R is
A{2,3,4,5,6}B(1,2,3,4,5)C{2,4,6}D{1,2,3,4,5,6}
If R = {(x,y):x,y∈W,x2+y2=25} , then find the domain and range of R .
View SolutionLet A = {2, 3, 4}, B ={3, 4, 5} be two sets and a relation R is defined from A to B is such that R ={(x, y) : x divides y, x∈A,y∈B} then domain of R is
View SolutionIf R={(x,y):x,y∈z,x2+y2≤4} is a relation defined on the set z of integers, then write domain and range.
View SolutionIf R={(x,y):x,y∈W,2x+y=8} ., then write the domain and range of R.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
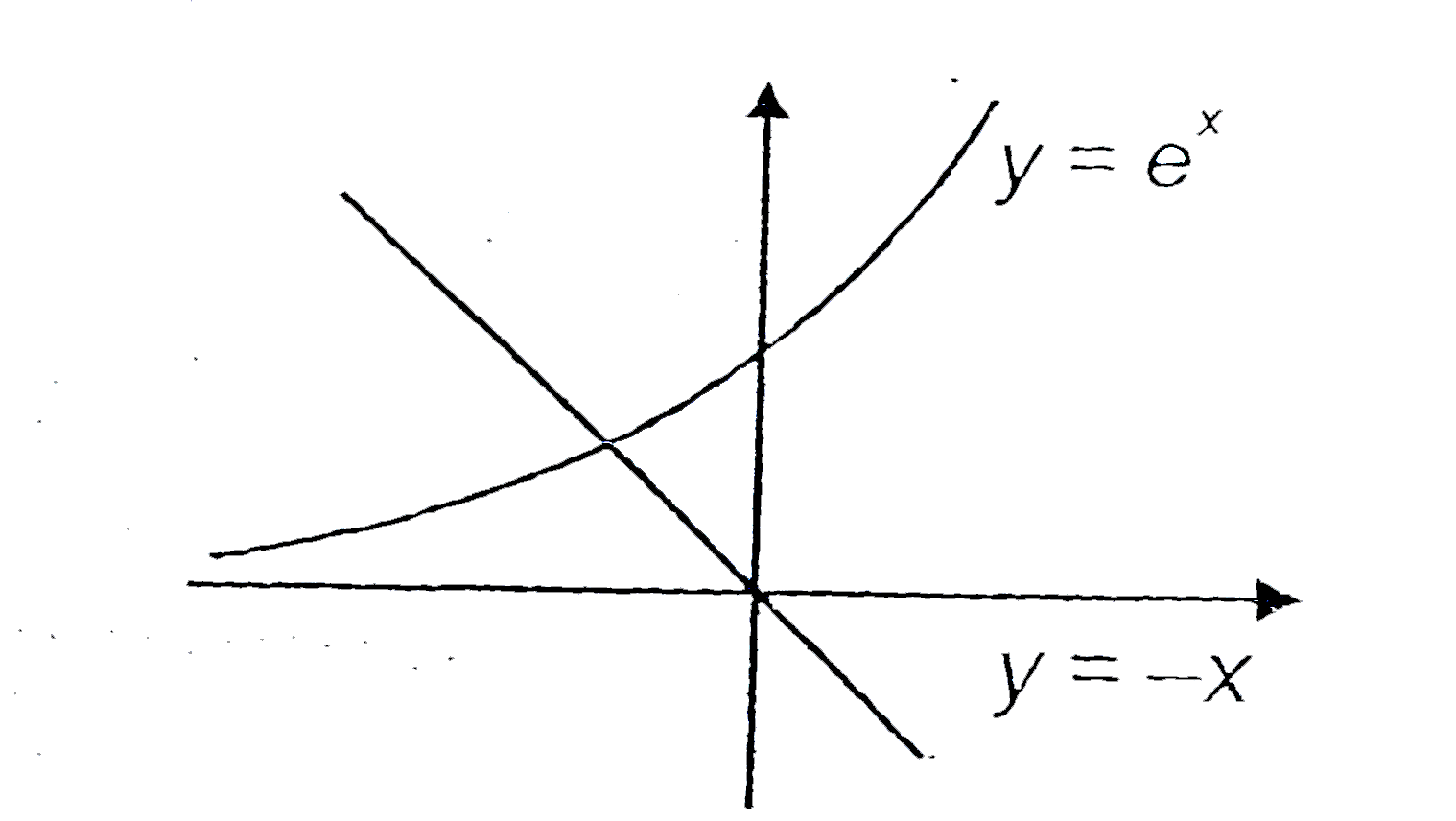
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
View Solution
