If S=16+192t−t3, then distance tavelled by the particle before coming to rest is
1040 units
520 units
260 units
2080 units
To find the distance traveled by the particle before it comes to rest, we will follow these steps:
Step 1: Find the velocity function
The position function is given as:
S=16+192t−t3
To find the velocity, we differentiate the position function with respect to time t:
v(t)=dSdt=ddt(16+192t−t3)
Calculating the derivative:
v(t)=0+192−3t2
So, the velocity function is:
v(t)=192−3t2
Step 2: Set the velocity to zero to find when the particle comes to rest
To find when the particle comes to rest, we set the velocity function equal to zero:
192−3t2=0
Rearranging gives:
3t2=192
Dividing both sides by 3:
t2=64
Step 3: Solve for t
Taking the square root of both sides:
t=±8
Since time cannot be negative, we take:
t=8
Step 4: Find the distance traveled at t=8
Now, we substitute t=8 back into the position function to find the distance traveled:
S(8)=16+192(8)−(8)3
Calculating each term:
S(8)=16+1536−512
Now, simplifying:
S(8)=16+1536−512=1040
Final Answer
The distance traveled by the particle before coming to rest is:
1040
---
The position function is given as:
S=16+192t−t3
To find the velocity, we differentiate the position function with respect to time t:
v(t)=dSdt=ddt(16+192t−t3)
Calculating the derivative:
v(t)=0+192−3t2
So, the velocity function is:
v(t)=192−3t2
To find when the particle comes to rest, we set the velocity function equal to zero:
192−3t2=0
Rearranging gives:
3t2=192
Dividing both sides by 3:
t2=64
Taking the square root of both sides:
t=±8
Since time cannot be negative, we take:
t=8
Now, we substitute t=8 back into the position function to find the distance traveled:
S(8)=16+192(8)−(8)3
Calculating each term:
S(8)=16+1536−512
Now, simplifying:
S(8)=16+1536−512=1040
The distance traveled by the particle before coming to rest is:
1040
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - APLICATIONS OF DERIVATIVESEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - I : CHAPTER 12)19videos
APLICATIONS OF DERIVATIVES
- BOOK - MARVEL PUBLICATIONCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - TEST YOUR GRASP11videos
APPLICATIONS OF DEFINITE INTEGRALS
Similar Questions
The position (in meters) of a particle moving on the x-axis is given by: x=2+9t+3t2−t3, where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionIf S=3t3+9t2+2t+7 , then distance travelled by the particle during the first second of its motion is
View Solution
Knowledge Check
- Question 1 - Select One
If S=16+(192)t−t3, then distance travelled by the particle before coming to rest is
A1040 unitsB520 unitsC260 unitsD2080 units - Question 2 - Select One
If S=13t3−4t2+12t, then distance travelled by the particle before it first comes to rest is
A323 unitsB32 unitsC643 unitsD64 units - Question 3 - Select One
A particle moves along a straight line on y-axis. The distance of the particle from O varies with time and is given by : y=20t−t2. The distance travelled by the particle before it momentarily comes to rest is
A200 mB100 mC50 mD150 m
The distance travelled by a motor car in t seconds after the brakes are applied is s feet where s=22t−12t2. The distance travelled by the car before it stops, is
View SolutionPosition vector of a particle moving in space is given by :
→r=3sintˆi+3costˆj+4tˆk
Distance travelled by the particle in 2s is :View SolutionA particle moves along a straight line OX. At a time t (in seconds) the distance x (in metre) of the particle is given by x=40+12t−t3. How long would the particle travel before coming to rest ?
View SolutionA particle moves along a straight line AB. At a time t (in seconds) the distance x (in metres) of the particle from O is given by x = 600 + 12t – t3. How long would the particle travel before coming to rest: -
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
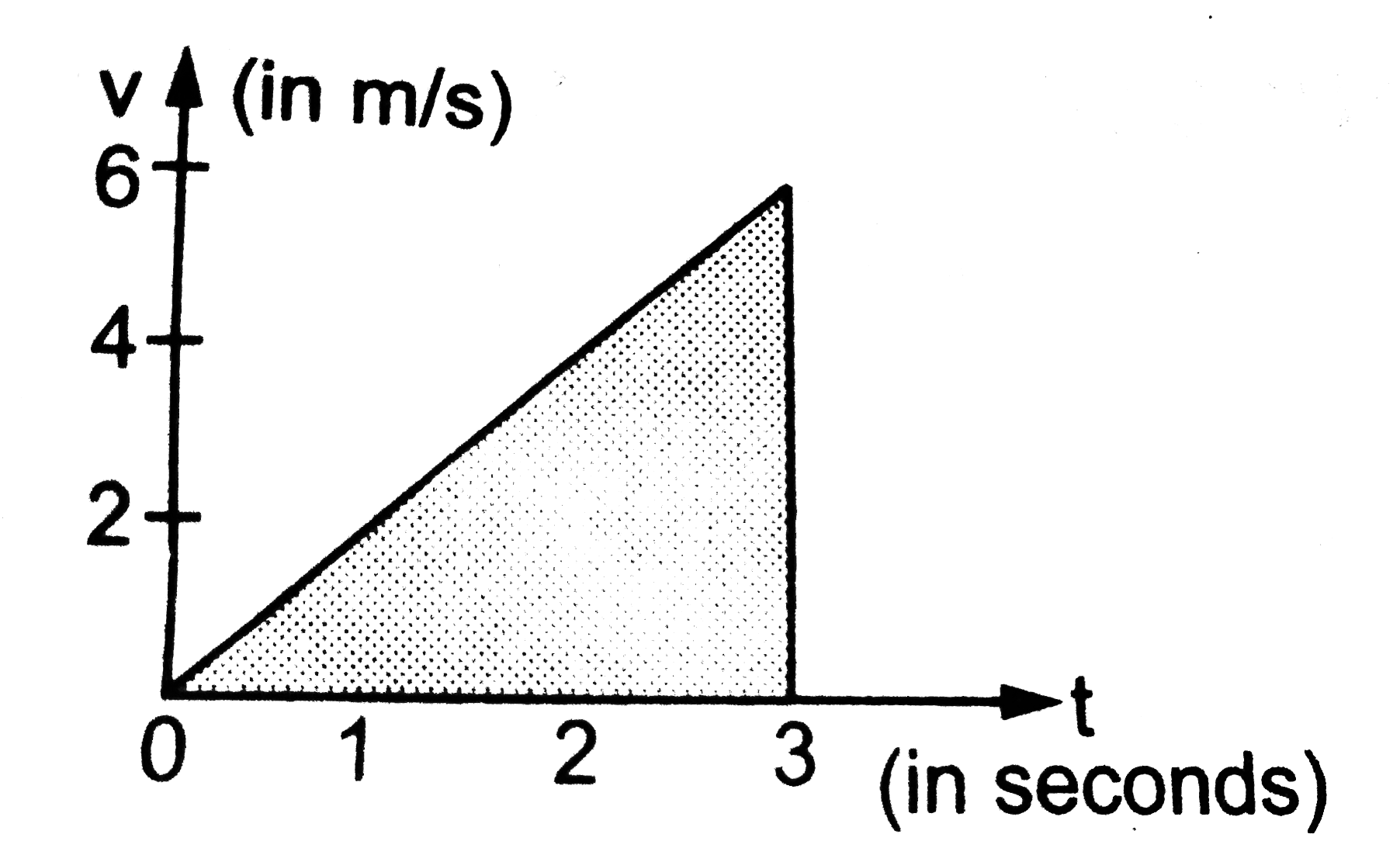 View Solution
View Solution

