If S2=at2+2bt+c, then the acceleration is : Solution in Kannada
Directly proportional to S
Inversely proportional to S
Directly proportional to S2
Inversely proportional to S3.
The correct Answer is:D
Step by step video, text & image solution for If S^(2)=at^(2)+2bt+c, then the acceleration is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - Latest Questions from AIEEE/JEE Examinations13videos
APPLICATION OF DERIVATIVES
- BOOK - MODERN PUBLICATIONCHAPTER - AREA UNDER CURVES EXERCISE - Recent Competitive Questions (Question from karnataka CET & COMED)9videos
AREA UNDER CURVES
Similar Questions
The equation of the tangent to the curve y=x+4x2, that is parallel to the x-axis, is :
05:26View SolutionThe area of the region bounded by the curves : y=x2 and y=4x−x2 in sq. units is :
04:38View SolutionThe distance covered by a particle moving in a straight line from a fixed point on the line is s, where s2=at2+2bt+⋅ Then prove that acceleration is proportional to s−3.
05:52View SolutionIf y=at^(2)+2bt+c and t=ax^(2)+2bx+c then (d^(2)y)/(dx^(2)) equals
03:49View SolutionIf y=at^(2)+2bt-c and t=ax^(2)+2bx+c then (d^(3)y)/(dx^(3)) equals
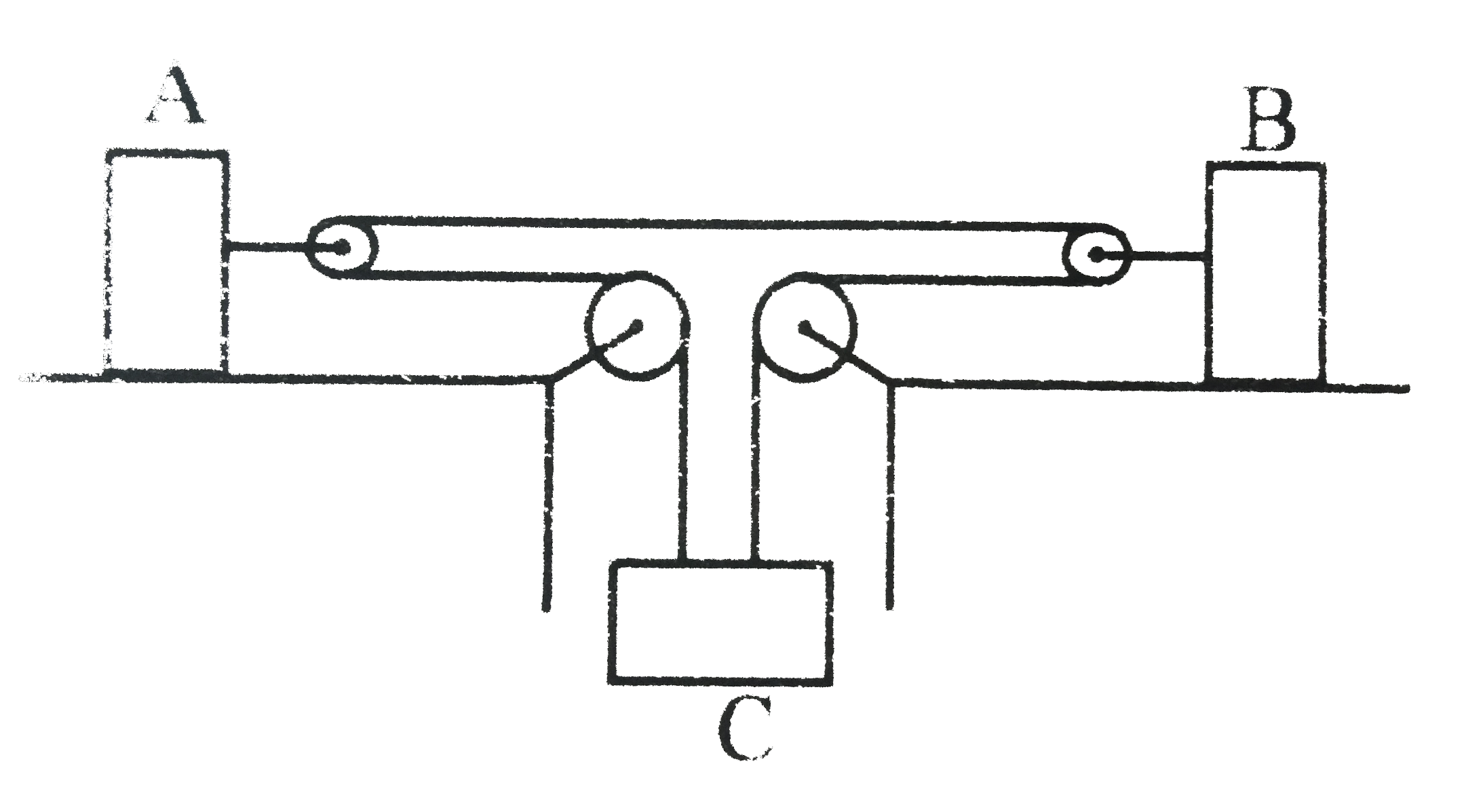
03:35View SolutionIn the figure acceleration of A is 1m/s2 upward, acceleration of B is 7m/s2 upward acceleration of C is 2m/s2 upward. The acceleration of D will be.
 07:32View Solution
07:32View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
 03:29View Solution
03:29View SolutionPosition of a particle as a function of time is given as x^2 = at^2 + 2bt + c , where a, b, c are constants. Acceleration of particle varies with x^(-n) then value of n is.
05:37View Solutionসরলরেখা বরাবর গতিশীল একটি কণার t সময়ে সরণ (x) নিম্নলিখিত সমীকরণটি থেকে পাওয়া যায়:x2=at2+2bt+c, যেখানে a,b এবং c ধ্রুবক।দেখাও যে, কণাটির ত্বরণ 1x3 এর সাথে সমানুপাতে পরিবর্তিত হয়।
03:57View SolutionThe displacement x of a particle in rectilinear motion at time t is represented as x2=at2+2bt+c, where a ,b, and c are constants. Show that the acceleration of this particle varies 1x3.
03:14View SolutionA particle is moving along a straight line path according to the relations s^(2)=at^(2)+2bt+c represent the distance travelled in t seconds and a, b, c are constant. Then the acceleration of the particle varies as:
02:56View SolutionIf S2=at2+2bt+c then the acceleration is
06:53View Solutionএকটি ক্ণার t সময়ে সরণ s ,s2=at2+2bt+cযেখানে, তাহলে কনার ত্বরন-এর সাথে s এর সম্পর্ক বের কর।
05:19View SolutionThe displacement x of a particle at time t moving along a straight line path is given by x^(2) = at^(2) + 2bt + c where a, b and c are constants. The acceleration of the particle varies as
04:40View SolutionA का बायी ओर त्वरण 2m/s2 है एवं B का बायी ओर त्वरण 1m/s2 है। C का त्वरण होगा
 07:13View Solution
07:13View Solution

