If sinA=b, what is the value of product sinA⋅cosA⋅tanA in terms of b?
1
1b
b
b2
The correct Answer is:D
To find the value of the product sinA⋅cosA⋅tanA in terms of b, where sinA=b, we can follow these steps:
Step 1: Write down the expression
We start with the expression we need to evaluate:
sinA⋅cosA⋅tanA
Step 2: Substitute the definition of tanA
Recall that tanA=sinAcosA. We can substitute this into our expression:
sinA⋅cosA⋅tanA=sinA⋅cosA⋅(sinAcosA)
Step 3: Simplify the expression
Now, we can simplify the expression:
sinA⋅cosA⋅(sinAcosA)=sinA⋅sinA⋅cosAcosA
The cosA in the numerator and denominator cancels out:
=sin2A
Step 4: Substitute sinA with b
Since we are given that sinA=b, we can substitute b into the expression:
sin2A=b2
Conclusion
Thus, the value of the product sinA⋅cosA⋅tanA in terms of b is:
b2
We start with the expression we need to evaluate:
sinA⋅cosA⋅tanA
Recall that tanA=sinAcosA. We can substitute this into our expression:
sinA⋅cosA⋅tanA=sinA⋅cosA⋅(sinAcosA)
Now, we can simplify the expression:
sinA⋅cosA⋅(sinAcosA)=sinA⋅sinA⋅cosAcosA
The cosA in the numerator and denominator cancels out:
=sin2A
Since we are given that sinA=b, we can substitute b into the expression:
sin2A=b2
Thus, the value of the product sinA⋅cosA⋅tanA in terms of b is:
b2
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
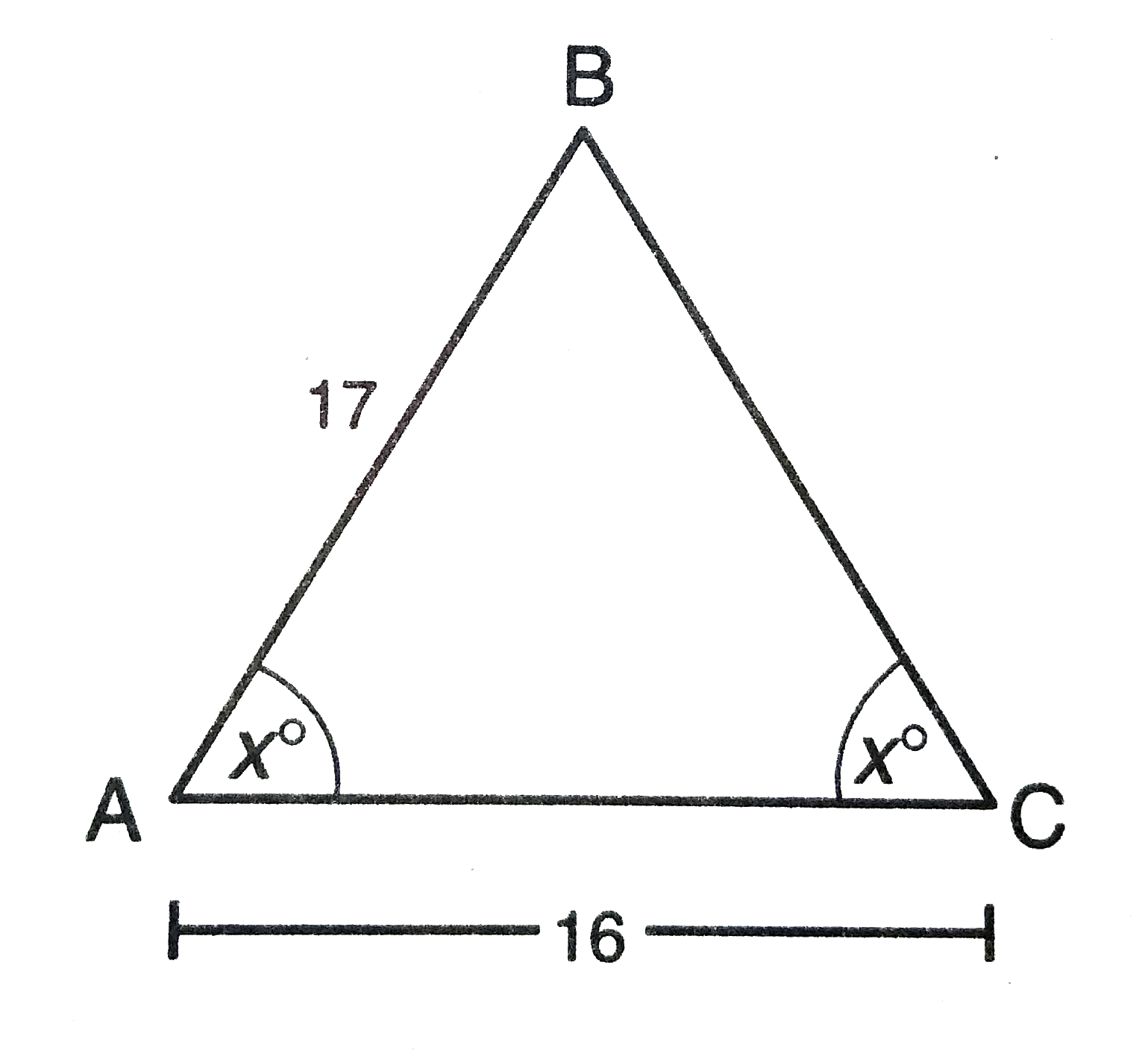
In the figure above, what is the value of sinA−cosA?
View SolutionIf sinA=cosA,then find the value of sin 2A.
View SolutionIf tanA=512, find the value of (sinA+cosA)secA .
View SolutionIf sinA=sinBandcosA=cosB, then find the value of A in terms of B.
View SolutionIf cosecA=2, find the value of 1tanA+sinA1+cosA
View SolutionIf cosA=0.6, find the value of 5sinA−3tanA.
View SolutionIf sec A= 2, then find the value of 1cotA+cosA1+sinA
View SolutionIf cosec A=2 , find the value of 1tanA+sinA1+cosA
View SolutionGiven that 16cotA=12 ; find the value of sinA+cosAsinA−cosA .
View SolutionIf 8tanA=15 , find sinA−cosA
View Solution
