If six students, including two particular students A and B, stand in a row, then the probability that A and B are separated with one student in between them is
8/15
1/5
2/15
4/15
The correct Answer is:D
Total number of ways in which 6 students can stand in row is 6!.
One student can stand between A and B in .4C1×2! ways.
Considering these three as one individual we have 4 students who can stand in a row in 4! Ways.
Therefore, number of ways in which one student is there between A and B and is .4C1×2!×4!.
Hence, required probability =.4C1×2!×4!6!=45
Topper's Solved these Questions
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section I - Solved Mcqs
126 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section- II (Assertion -Reason Types MCQs)
15 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test
50 Videos
Similar Questions
Ten students are seated at random in a row. The probability that two particular students are not seated side by side is 4/5.
View SolutionIf 15 different prizes have been distributed among 5 students equally, then the probability that two specified prizes are received by one student only is
View Solution
Knowledge Check
In a school, all the students can stand in a row, so that each row has 5, 9 or 10 students. Find the least number of students in the school.
A90B95C85D100The heights (in cm) of 50 students of a class are given below
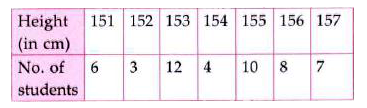
One student is selected at random. Find the probability that the height of the selected student is 157 cm.A3/50B2/25C8/25D7/50In a row of 50 students Renu is fifteenth from left and Raju is eighteenth from right. How many students are between them?
A17B15C7D8
A college student has to appear for two examinations A and B. The probabilities that the student passes in A and B are 2/3 and 3/4 respectively. If it is known that the student passes at least one among the two examinations, then the probability that the student will pass both the examination is (A) 1/6 (B) 1/2 (C) 1/3 (D) 6/11
View SolutionTen IIT students and 2 DCE students sit in a row. The number of ways in which exactly 3 IIT students sit in between 2 DCE students
View SolutionIt is given that in a group of 3 students the probability of 2 students not having the same birthday is 0.922 . What is the probability that the 2 students have the same birthday ?
View SolutionSuppose that six students, including Madhu and Puja, are having six beds arranged in a row. Further, suppose that Mudhu does not want a bed adjacent to Puja. Then the number of ways, the beds can be allotted to students is
View SolutionLet there are 4 sections of 25 students each in a coaching class. Now, out of 150 students 100 are to be selected randomly and entrolled in these sections. Then, the probability that the students A and B (both present in 150 students) are selected and placed in the same section, is
View Solution
