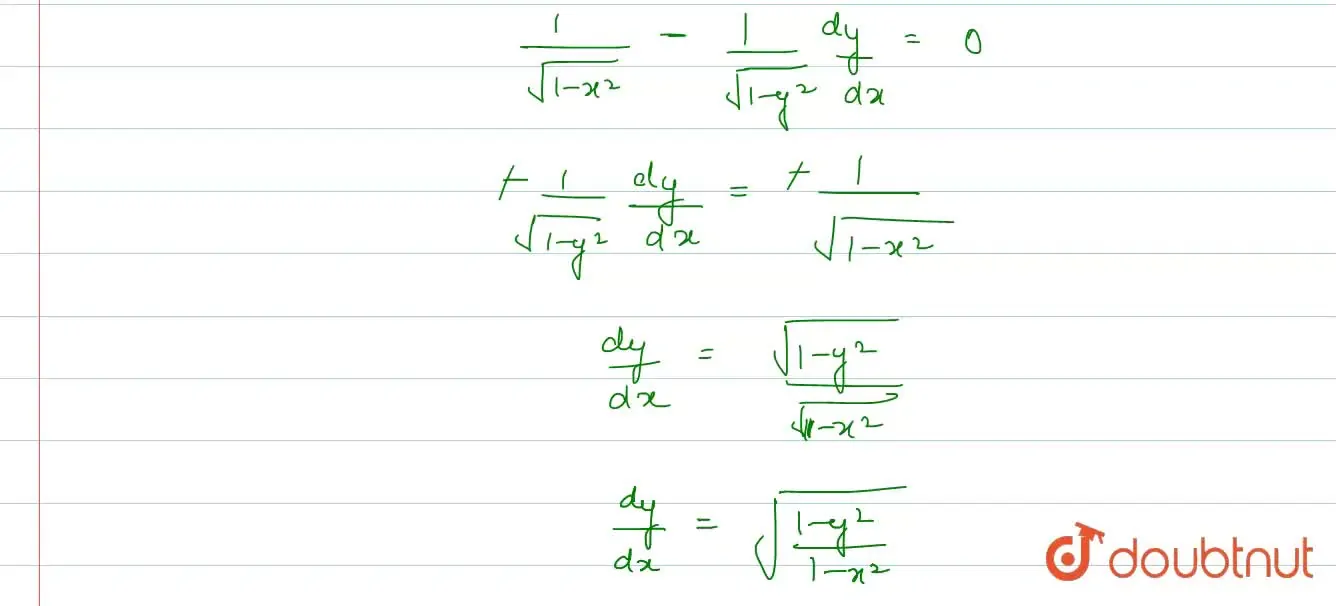If , then prove that
Video Solution
Text Solution
The correct Answer is:N/a
We have,
On putting and , we get
,
On differentiating both sides w.r.t.x, we get
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If √1−x2+√1−y2=a(x−y), prove that dydx=√1−y21−x2
View SolutionIf √1−x2+√1−y2=a(x−y), prove that dydx=√1−y21−x2
View SolutionIf √1−x2+√1−y2=a(x−y),provethatdydx=√1−y21−x2
View SolutionIf √1−x4+√1−y4=k(x2−y2), prove that dydx=x√1−y4y√1−x4
View SolutionIf y√1−x2+x√1−y2=1. Prove that dydx=−√1−y21−x2
View SolutionIf √1−x6+√1−y6=a(x3−y3), then prove that dydx=x2y2√1−y61−x6
View SolutionIf y√1−x2+x√1−y2=1,p r o v et h a tdydx=√1−y21−x2.
View SolutionIf y√1−x2+x√1−y2=1 show that dydx=−√1−y21−x2
View SolutionIf √1−x2+√1−y2=a(x−y), then dydx equals
View SolutionIf y=xcos−1x√1−x2−log√1−x2, then prove that dydx=cos−1x(1−x2)32
View Solution